Integers, a fundamental concept in mathematics, are whole numbers that include positive numbers, negative numbers, and zero. They are denoted by the symbol Z\mathbb{Z}Z, derived from the German word Zahlen, meaning “numbers.” Integers are crucial for understanding arithmetic, algebra, and advanced mathematical concepts, serving as a foundation for both theoretical and applied mathematics.
What are Integers?
Integers are a set of numbers that include:
- Positive integers: 1,2,3,…
- Negative integers: −1,−2,−3,…
- Zero: 000
Unlike fractions or decimals, integers do not include parts or divisions of a whole number. For instance, 3 is an integer, but 3.5 is not.
Properties of Integers
Integers possess several key properties that make them indispensable in mathematics:
Closure Property:
The sum, difference, or product of two integers is always an integer. For example:
3+(−5) = −2, and 4×(−3) = −12.
Commutative Property:
- The addition and multiplication of integers are commutative, meaning the order does not affect the result:
a+b = b+a, and a×b = b×a. - However, subtraction and division are not commutative.
Associative Property:
The grouping of integers does not change the result for addition and multiplication:
(a+b)+c = a+(b+c), and (a×b)×c = a×(b×c).
Identity Element:
- The additive identity is 0, as adding zero to any integer does not change its value:
a+0 = a. - The multiplicative identity is 111, as multiplying any integer by 1 gives the same integer:
a×1 = a.
Distributive Property:
Multiplication distributes over addition or subtraction:
a×(b+c) = (a×b)+(a×c).
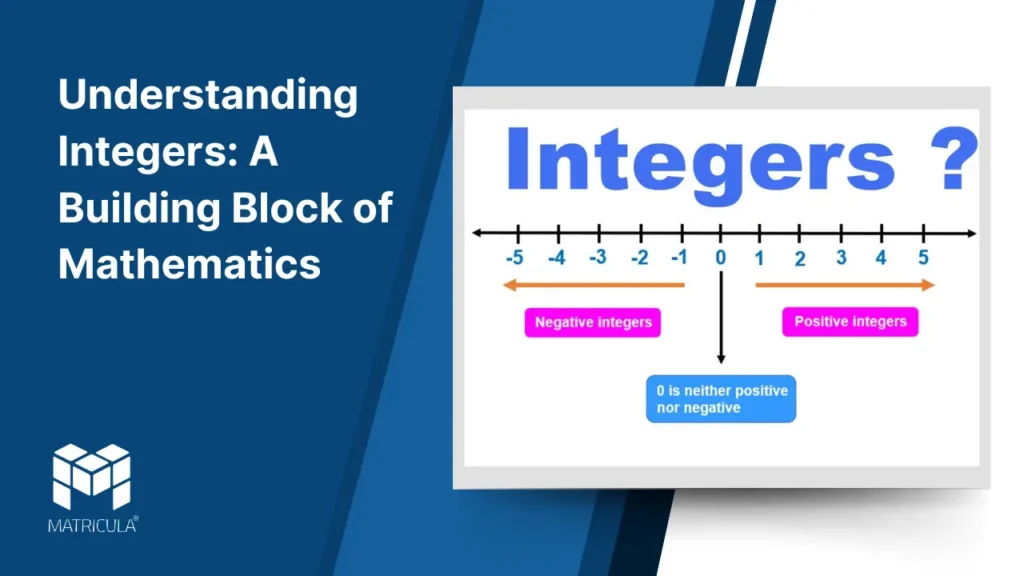
Representation of Integers on the Number Line
Integers can be represented on a number line, where:
- Positive integers lie to the right of zero.
- Negative integers lie to the left of zero.
- Zero serves as the central reference point.
The number line visually demonstrates the order and magnitude of integers, aiding in operations like addition and subtraction.
Applications of Integers
Integers play a vital role in various fields:
- Everyday Life: Representing temperatures, bank balances (debits and credits), and elevations (above or below sea level).
- Mathematics: Serving as the basis for operations in algebra, equations, and inequalities.
- Computer Science: Used in programming, algorithms, and data structures.
- Physics: Representing directions (positive or negative) and quantities like charges.
Importance in Advanced Mathematics
Integers are a subset of the real numbers and serve as the foundation for more complex number systems, including rational numbers, irrational numbers, and complex numbers. They are essential for exploring modular arithmetic, number theory, and cryptography.