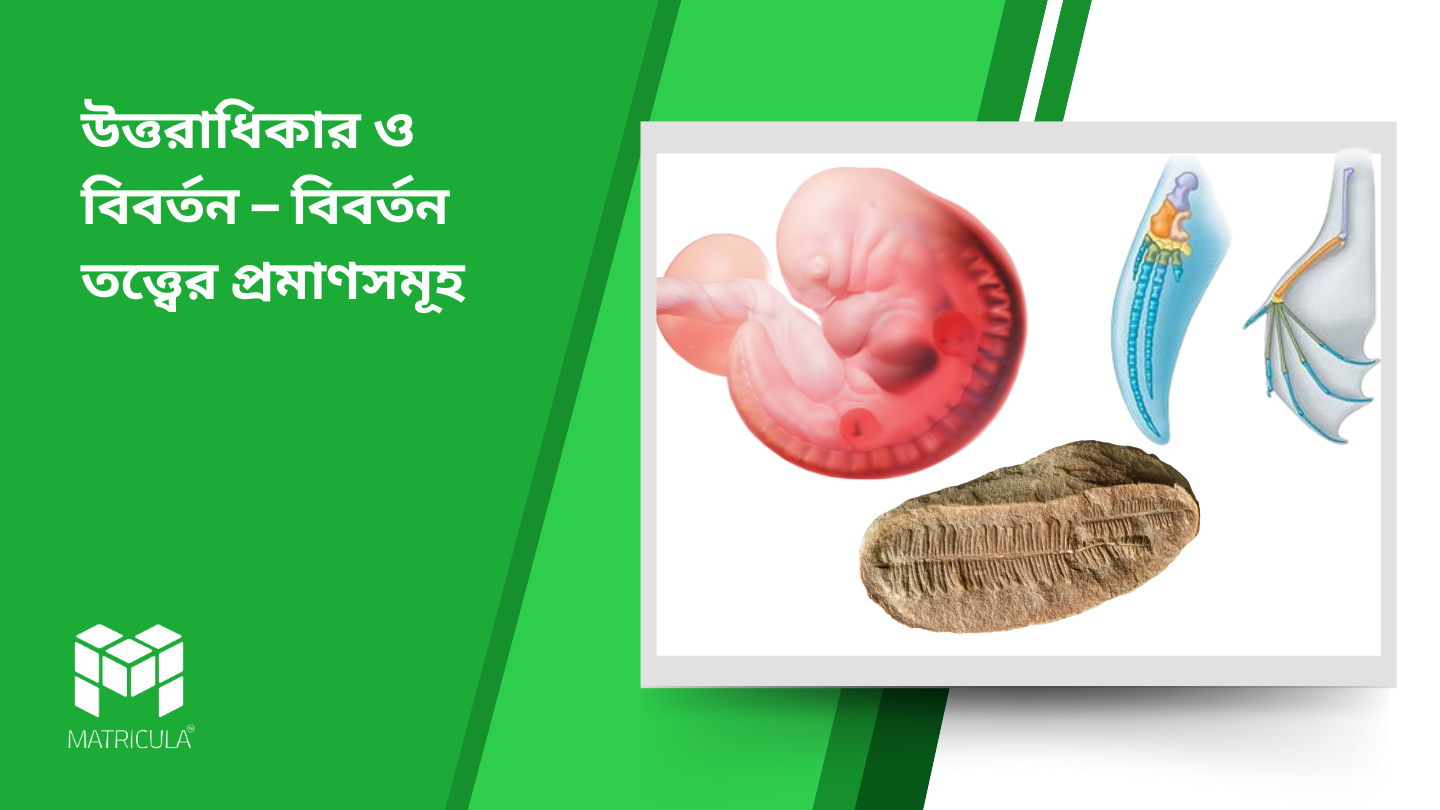
Evolution – Evidences for the Theory of Evolution
Introduction Evolution is a fundamental concept in biology that explains how life has changed and diversified over millions of years. The theory of evolution, primarily
Latest Articles
Evolution – Evidences for the Theory of Evolution
Introduction Evolution is a fundamental concept in biology that explains how life has changed and diversified over millions of years. The theory of evolution, primarily
Evolution – Neo-Darwinism & Errors of Darwinism
Introduction Evolution is the process through which organisms undergo gradual changes over generations, leading to the diversity of life on Earth. Charles Darwin’s theory of
Theory of Darwin or Darwinism
Class 10 Biology – West Bengal Board Introduction Darwin’s theory of evolution, also known as Darwinism, was proposed by Charles Darwin in his book On
Biology concepts:
Biodiversity encompasses the variety of life on Earth, including all organisms, species, and ecosystems. It plays a crucial role in maintaining the balance and health of our planet’s ecosystems. Among the different levels of biodiversity, species diversity—the variety of species within a habitat—is particularly vital to ecosystem functionality and resilience. However, human activities and environmental changes have significantly impacted biodiversity, leading to its decline. This article explores the importance of species diversity, the causes of biodiversity loss, and its effects on ecosystems and human well-being.
Importance of Species Diversity to the Ecosystem
Species diversity is a cornerstone of ecosystem health. Each species has a unique role, contributing to ecological balance and providing critical services such as:
Ecosystem Stability: Diverse ecosystems are more resilient to environmental changes and disturbances, such as climate change or natural disasters. A variety of species ensures that ecosystems can adapt and recover efficiently.
Nutrient Cycling and Productivity: Different species contribute to nutrient cycling, soil fertility, and overall productivity. For instance, plants, fungi, and decomposers recycle essential nutrients back into the soil.
Pollination and Seed Dispersal: Pollinators like bees and birds facilitate plant reproduction, while seed dispersers ensure the spread and growth of vegetation.
Climate Regulation: Forests, wetlands, and oceans—supported by diverse species—act as carbon sinks, regulating the Earth’s temperature and mitigating climate change.
Human Benefits: Biodiversity provides resources such as food, medicine, and raw materials. Cultural, recreational, and aesthetic values also stem from species diversity.
Causes of Loss of Biodiversity
Several factors, most of which are anthropogenic, contribute to biodiversity loss:
Habitat Destruction: Urbanization, deforestation, and agriculture often result in habitat fragmentation or complete destruction, leading to the displacement and extinction of species.
Climate Change: Altered temperature and precipitation patterns disrupt ecosystems, forcing species to adapt, migrate, or face extinction.
Pollution: Contamination of air, water, and soil with chemicals, plastics, and waste harms wildlife and degrades habitats.
Overexploitation: Unsustainable hunting, fishing, and logging deplete species populations faster than they can recover.
Invasive Species: Non-native species introduced intentionally or accidentally often outcompete native species, leading to ecological imbalances.
Diseases: Pathogens and pests can spread rapidly in altered or stressed ecosystems, further threatening species.
Effects of Loss of Biodiversity
The decline in biodiversity has profound and far-reaching consequences:
Ecosystem Collapse: Loss of keystone species—those crucial to ecosystem functioning—can trigger the collapse of entire ecosystems.
Reduced Ecosystem Services: Biodiversity loss undermines services like pollination, water purification, and climate regulation, directly affecting human livelihoods.
Economic Impacts: Declines in biodiversity affect industries such as agriculture, fisheries, and tourism, resulting in economic losses.
Food Security Risks: The reduction in plant and animal diversity threatens food supply chains and agricultural resilience.
Health Implications: Loss of species reduces the potential for medical discoveries and increases vulnerability to zoonotic diseases as ecosystems degrade.
Ecosystems are dynamic systems formed by the interaction of living and non-living components. These components can be categorized into biotic and abiotic factors. Together, they shape the structure, functionality, and sustainability of ecosystems. Understanding these factors is crucial to studying ecology, environmental science, and the intricate relationships within nature.
Biotic Factors
Biotic factors are the living components of an ecosystem. These include organisms such as plants, animals, fungi, bacteria, and all other life forms that contribute to the biological aspect of the environment.
Categories of Biotic Factors:
Producers (Autotrophs): Organisms like plants and algae that synthesize their own food through photosynthesis or chemosynthesis.
Consumers (Heterotrophs): Animals and other organisms that rely on consuming other organisms for energy. They can be herbivores, carnivores, omnivores, or decomposers.
Decomposers and Detritivores: Fungi and bacteria that break down dead organic matter, recycling nutrients back into the ecosystem.
Role of Biotic Factors:
Energy Flow: Producers, consumers, and decomposers drive energy transfer within an ecosystem.
Interdependence: Interactions like predation, competition, mutualism, and parasitism maintain ecological balance.
Population Regulation: Species interactions regulate populations, preventing overpopulation and resource depletion.
Examples of Biotic Interactions:
- Pollinators like bees and butterflies aid in plant reproduction.
- Predator-prey relationships, such as lions hunting zebras.
- Symbiotic relationships, such as fungi and algae forming lichens.
Abiotic Factors
Abiotic factors are the non-living physical and chemical components of an ecosystem. They provide the foundation upon which living organisms thrive and evolve.
Key Abiotic Factors:
Climate: Temperature, humidity, and precipitation influence species distribution and survival.
Soil: Nutrient composition, pH levels, and texture affect plant growth and the organisms dependent on plants.
Water: Availability, quality, and salinity determine the survival of aquatic and terrestrial life.
Sunlight: Essential for photosynthesis and influencing the behavior and physiology of organisms.
Air: Oxygen, carbon dioxide, and other gases are critical for respiration and photosynthesis.
Impact of Abiotic Factors:
Habitat Creation: Abiotic conditions define the types of habitats, such as deserts, forests, and aquatic zones.
Species Adaptation: Organisms evolve traits to adapt to specific abiotic conditions, like camels surviving in arid climates.
Ecosystem Dynamics: Abiotic changes, such as droughts or temperature shifts, can significantly alter ecosystems.
Examples of Abiotic Influence:
- The role of sunlight and CO2 in photosynthesis.
- River currents shaping aquatic habitats.
- Seasonal temperature changes triggering animal migration.
Interactions Between Biotic and Abiotic Factors
Biotic and abiotic factors are interconnected, influencing each other to maintain ecosystem equilibrium. For example:
- Plants (biotic) rely on soil nutrients, water, and sunlight (abiotic) to grow.
- Animals (biotic) depend on water bodies (abiotic) for hydration and food sources.
- Abiotic disturbances like hurricanes can affect biotic populations by altering habitats.
Respiration is a fundamental biological process through which living organisms generate energy to power cellular functions. It occurs in two main forms: aerobic and anaerobic respiration. While both processes aim to produce energy in the form of adenosine triphosphate (ATP), they differ significantly in their mechanisms, requirements, and byproducts. This article delves into the definitions, processes, and differences between aerobic and anaerobic respiration.
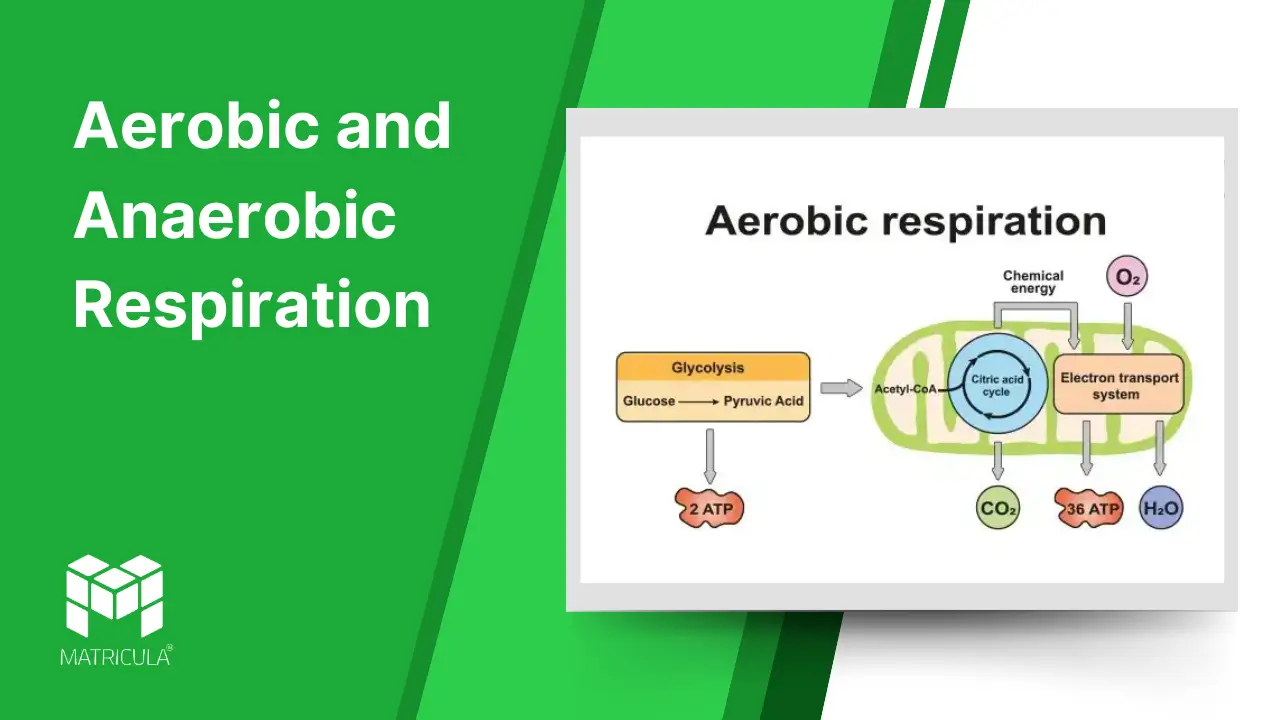
Aerobic Respiration
Aerobic respiration is the process of breaking down glucose in the presence of oxygen to produce energy. It is the most efficient form of respiration, generating a high yield of ATP.
Process:
- Glycolysis: The breakdown of glucose into pyruvate occurs in the cytoplasm, yielding 2 ATP and 2 NADH molecules.
- Krebs Cycle (Citric Acid Cycle): Pyruvate enters the mitochondria, where it is further oxidized, producing CO2, ATP, NADH, and FADH2.
- Electron Transport Chain (ETC): NADH and FADH2 donate electrons to the ETC in the mitochondrial membrane, driving the production of ATP through oxidative phosphorylation. Oxygen acts as the final electron acceptor, forming water.
Equation:
• Glucose (C6H12O6) + Oxygen (6O2) → Carbon dioxide (6CO2) + Water (6H2O) + Energy (36-38 ATP)
Byproducts: Carbon dioxide and water.
Efficiency: Produces 36-38 ATP molecules per glucose molecule.
Anaerobic Respiration
Anaerobic respiration occurs in the absence of oxygen, relying on alternative pathways to generate energy. While less efficient than aerobic respiration, it is vital for certain organisms and under specific conditions in multicellular organisms.
Process:
- Glycolysis: Similar to aerobic respiration, glucose is broken down into pyruvate in the cytoplasm, yielding 2 ATP and 2 NADH molecules.
- Fermentation: Pyruvate undergoes further processing to regenerate NAD+, enabling glycolysis to continue. The pathway varies depending on the organism:
- Lactic Acid Fermentation: Pyruvate is converted into lactic acid (e.g., in muscle cells during intense exercise).
- Alcoholic Fermentation: Pyruvate is converted into ethanol and CO2 (e.g., in yeast cells).
Equation (Lactic Acid Fermentation):
• Glucose (C6H12O6) → Lactic acid (2C3H6O3) + Energy (2 ATP)
Byproducts: Lactic acid or ethanol and CO2, depending on the pathway.
Efficiency: Produces only 2 ATP molecules per glucose molecule.
Key Differences Between Aerobic and Anaerobic Respiration
| Aspect | Aerobic Respiration | Anaerobic Respiration |
| Oxygen Requirement | Requires oxygen | Occurs in absence of oxygen |
| ATP Yield | 36-38 ATP per glucose molecule | 2 ATP per glucose molecule |
| Location | Cytoplasm and mitochondria | Cytoplasm only |
| Byproducts | Carbon dioxide and water | Lactic acid or ethanol and CO2 |
| Efficiency | High | Low |
Applications and Importance
Aerobic Respiration:
- Essential for sustained energy production in most plants, animals, and other aerobic organisms.
- Supports high-energy-demand activities, such as physical exercise and metabolic processes.
Anaerobic Respiration:
Enables survival during oxygen deficits, as seen in muscle cells during vigorous activity.
Crucial in environments lacking oxygen, such as deep soil layers or aquatic sediments.
Used in industries for fermentation processes, producing bread, beer, and yogurt.
The animal cell is one of the fundamental units of life, playing a pivotal role in the biological processes of animals. It is a eukaryotic cell, meaning it possesses a well-defined nucleus enclosed within a membrane, along with various specialized organelles. Let’s explore its shape and size, structural components, and types in detail.
Shape and Size of Animal Cells
Animal cells exhibit a variety of shapes and sizes, tailored to their specific functions. Unlike plant cells, which are typically rectangular due to their rigid cell walls, animal cells are more flexible and can be spherical, oval, flat, elongated, or irregularly shaped. This flexibility is due to the absence of a rigid cell wall, allowing them to adapt to different environments and functions.
- Size: Animal cells are generally microscopic, with sizes ranging from 10 to 30 micrometers in diameter. Some specialized cells, like nerve cells (neurons), can extend over a meter in length in larger organisms.
- Shape: The shape of an animal cell often reflects its function. For example, red blood cells are biconcave to optimize oxygen transport, while neurons have long extensions to transmit signals efficiently.
Structure of Animal Cells
Animal cells are composed of several key components, each performing specific functions essential for the cell’s survival and activity. Below are the major structural elements:
Cell Membrane (Plasma Membrane):
- A semi-permeable membrane is made up of a lipid bilayer with embedded proteins.
- Regulates the entry and exit of substances, maintaining homeostasis.
Cytoplasm:
- A jelly-like substance that fills the cell, provides a medium for biochemical reactions.
- Houses the organelles and cytoskeleton.
Nucleus:
- The control center of the cell, containing genetic material (DNA) organized into chromosomes.
- Surrounded by the nuclear envelope, it regulates gene expression and cell division.
Mitochondria:
- Known as the powerhouse of the cell, mitochondria generate energy in the form of ATP through cellular respiration.
Endoplasmic Reticulum (ER):
- Rough ER: Studded with ribosomes, it synthesizes proteins.
- Smooth ER: Involved in lipid synthesis and detoxification processes.
Golgi Apparatus:
- Modifies, sorts, and packages proteins and lipids for transport.
Lysosomes:
- Contain digestive enzymes to break down waste materials and cellular debris.
Cytoskeleton:
- A network of protein fibers providing structural support and facilitating intracellular transport and cell division.
Centrioles:
- Cylindrical structures are involved in cell division, forming the spindle fibers during mitosis.
Ribosomes:
- Sites of protein synthesis, either free-floating in the cytoplasm or attached to the rough ER.
Vesicles and Vacuoles:
- Vesicles transport materials within the cell, while vacuoles store substances, though they are smaller and less prominent compared to those in plant cells.
Types of Animal Cells
Animal cells are specialized to perform various functions, leading to the existence of different types. Below are some primary examples:
Epithelial Cells:
- Form the lining of surfaces and cavities in the body, offering protection and enabling absorption and secretion.
Muscle Cells:
- Specialized for contraction, and facilitating movement. They are categorized into skeletal, cardiac, and smooth muscle cells.
Nerve Cells (Neurons):
- Electrical signals are transmitted throughout the body, enabling communication between different parts.
Red Blood Cells (Erythrocytes):
- Transport oxygen and carbon dioxide using hemoglobin.
White Blood Cells (Leukocytes):
- Play a critical role in immune response by defending the body against infections.
Reproductive Cells (Gametes):
- Sperm cells in males and egg cells in females are involved in reproduction.
Connective Tissue Cells:
Include fibroblasts, adipocytes, and chondrocytes, contributing to structural support and storage functions.
Diffusion and osmosis are fundamental processes that facilitate the movement of molecules in biological systems. While both involve the movement of substances, they differ in their mechanisms, requirements, and specific roles within living organisms. Understanding these differences is crucial for comprehending various biological and chemical phenomena.
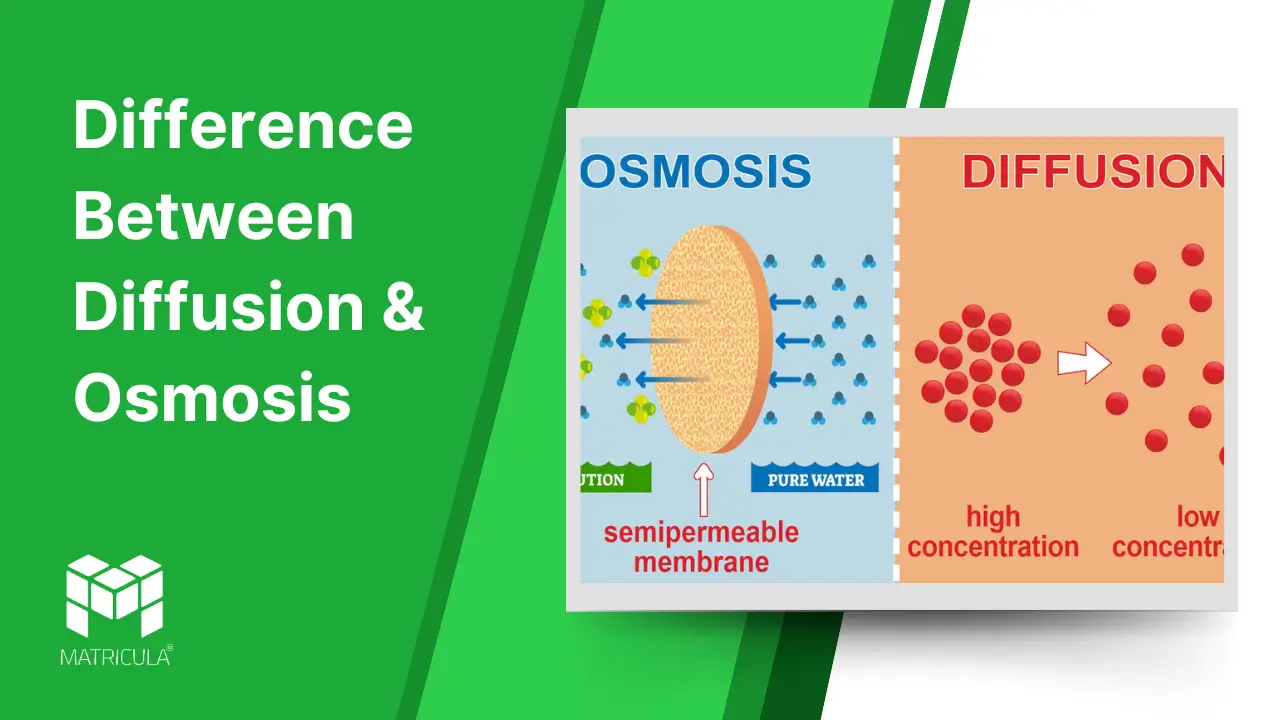
What is Diffusion?
Diffusion is the process by which molecules move from an area of higher concentration to an area of lower concentration until equilibrium is reached. This process occurs due to the random motion of particles and does not require energy input.
Key Characteristics:
Can occur in gases, liquids, or solids.
- Does not require a semipermeable membrane.
- Driven by the concentration gradient.
Examples:
- The diffusion of oxygen and carbon dioxide across cell membranes during respiration.
- The dispersion of perfume molecules in the air.
Importance in Biology:
- Enables the exchange of gases in the lungs and tissues.
- Facilitates the distribution of nutrients and removal of waste products in cells.
What is Osmosis?
Osmosis is the movement of water molecules through a semipermeable membrane from an area of lower solute concentration to an area of higher solute concentration. It aims to balance solute concentrations on both sides of the membrane.
Key Characteristics:
- Specific to water molecules.
- Requires a semipermeable membrane.
- Driven by differences in solute concentration.
Examples:
- Absorption of water by plant roots from the soil.
- Water movement into red blood cells placed in a hypotonic solution.
Importance in Biology:
- Maintains cell turgor pressure in plants.
- Regulates fluid balance in animal cells.
Key Differences Between Diffusion and Osmosis
| Aspect | Diffusion | Osmosis |
| Definition | Movement of molecules from high to low concentration. | Movement of water across a semipermeable membrane from low to high solute concentration. |
| Medium | Occurs in gases, liquids, and solids. | Occurs only in liquids. |
| Membrane Requirement | Does not require a membrane. | Requires a semipermeable membrane. |
| Molecules Involved | Involves all types of molecules. | Specific to water molecules. |
| Driving Force | Concentration gradient. | Solute concentration difference. |
| Examples | Exchange of gases in the lungs. | Absorption of water by plant roots. |
Similarities Between Diffusion and Osmosis
Despite their differences, diffusion and osmosis share several similarities:
- Both are passive processes, requiring no energy input.
- Both aim to achieve equilibrium in concentration.
- Both involve the movement of molecules driven by natural gradients.
Applications and Significance
- In Plants:
- Osmosis helps plants absorb water and maintain structural integrity through turgor pressure.
- Diffusion facilitates gas exchange during photosynthesis and respiration.
- In Animals:
- Osmosis regulates hydration levels and prevents cell bursting or shrinking.
- Diffusion ensures efficient oxygen delivery and carbon dioxide removal in tissues.
- In Everyday Life:
- Water purification systems often use osmotic principles.
- Diffusion explains the spread of substances like pollutants in the environment.
Chemistry concepts:
From Shine to Decay: Navigating the Intricacies of Rusting and Corrosion
Introduction:
Rusting and corrosion are ubiquitous natural processes that can lead to the deterioration of metals, impacting structures, equipment, and infrastructure. While often used interchangeably, rusting and corrosion encompass distinct phenomena. This article delves into the mechanisms of rusting and corrosion, highlighting their differences, exploring protective measures, and shedding light on the significance of these processes in the context of iron and other metals.
Understanding Corrosion and Rusting:
Corrosion and rusting are two terms used to describe the deterioration of materials caused by chemical or electrochemical reactions, with their surroundings. Rusting specifically refers to the process in which iron or iron alloys react with oxygen and water resulting in the formation of iron oxide, commonly known as rust. Essentially rusting is a type of corrosion that specifically affects materials containing iron.
Process of Corrosion and Rusting:
Corrosion and rusting typically occur due, to oxidation reactions;
Corrosion; When metals come into contact with an environment that contains oxygen and other corrosive substances they undergo oxidation. This leads to the formation of metal oxides or other compounds that gradually weaken the materials structure.
Rusting; In the case of iron rusting happens when iron reacts, with both oxygen and water. During this process the iron atoms lose electrons. Get oxidized, resulting in the formation of brown rust known as iron oxide (Fe2O3 or Fe3O4).
Differentiating Corrosion and Rusting:
While all rusting involves corrosion, not all forms of corrosion result in rust. Corrosion can take various forms depending on the metal, environment, and conditions. For instance, aluminium corrodes but does not produce rust. Rusting, however, is specific to iron and iron alloys.
Preventing Corrosion and Rusting:
Mitigating the effects of corrosion and rusting involves several strategies:
Protective Coatings:
Applying coatings like paint, zinc, or polymer layers forms a barrier that shields the metal from contact with corrosive agents.
Galvanization:
Coating iron with a layer of zinc through galvanization forms a protective zinc oxide layer that prevents iron from reacting with the environment.
Inhibitors:
Rust and corrosion inhibitors, such as chemicals or compounds added to materials, slow down or prevent the oxidation process. These inhibitors can be organic or inorganic and are used in various industries.
Significance of Corrosion and Rusting:
The importance of corrosion and rust cannot be underestimated. It is crucial to comprehend these phenomena in order to protect the durability of structures, machinery and equipment. If left unaddressed, rust can cause failures, escalate maintenance expenses and jeopardize safety, in industries, like construction, marine sectors.
Conclusion:
The interaction between materials and their environment is highlighted by rusting and corrosion. While corrosion encompasses a range, rusting specifically affects iron and iron alloys. By gaining an understanding of these processes scientists, engineers and industries can devise approaches to prevent and minimize the harmful consequences of rusting and corrosion. Through coatings and corrosion inhibitors the ongoing mission to combat rusting and corrosion guarantees the endurance and strength of structures and materials, in our contemporary world.
Beyond the Periodic Table: Electronegativity’s Hidden Stories of Element Bonds
Introduction:
Electronegativity, a fundamental concept in chemistry, unveils the intricate interactions between atoms in molecules. It governs the distribution of electrons within compounds, influencing chemical bonding, polarity, and reactivity. This article explores the essence of electronegativity, the most electronegative element, the electronegative elements’ order, and the electronegativity series that shapes our understanding of chemical phenomena.
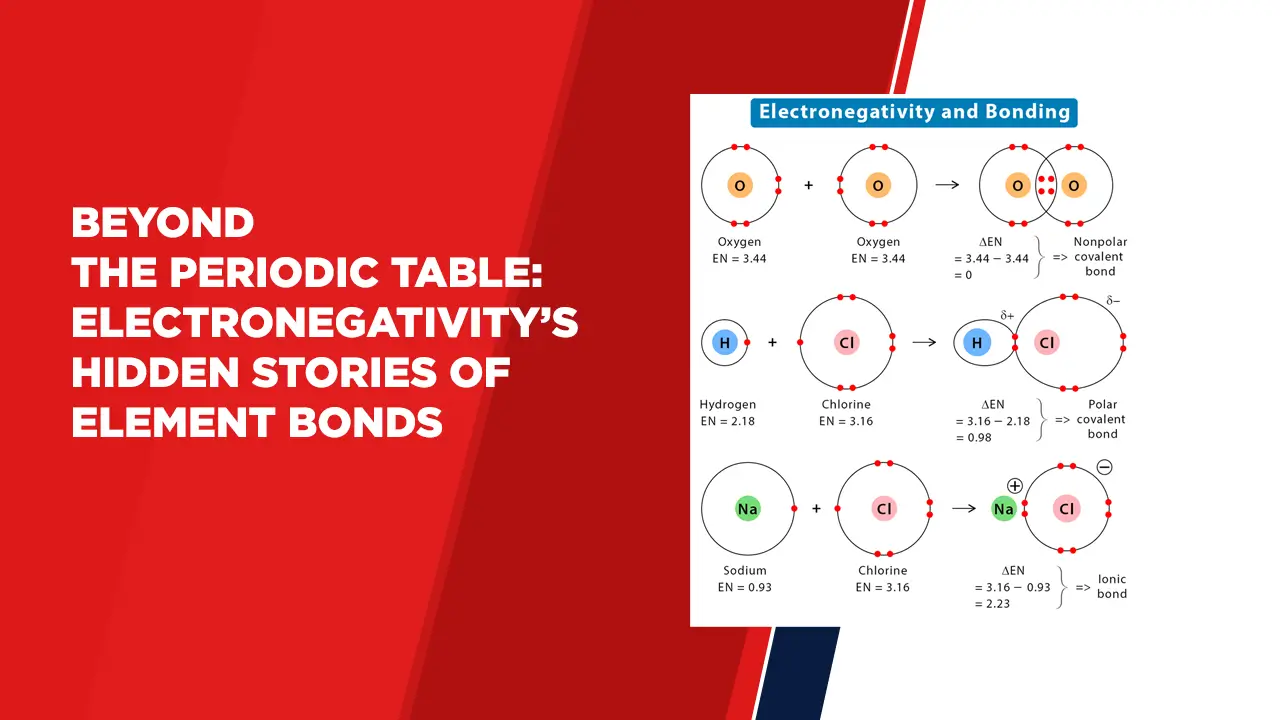
Defining Electronegativity:
Electronegativity is the measure of an atom’s ability to attract and retain electrons within a chemical bond. It characterises the atom’s affinity for electrons in a covalent or polar bond, affecting the sharing or transfer of electrons between atoms.
The Most Electronegative Element:
Fluorine, with an electronegativity value of 3.98 on the Pauling scale, stands as the most electronegative element. Its strong electron-attracting ability results from its small atomic size and high effective nuclear charge.
Order of Electronegative Elements:
Electronegativity values follow a predictable trend across the periodic table, generally increasing from left to right across a period and decreasing from top to bottom within a group. This pattern reflects the atomic structure’s influence on an atom’s attraction for electrons.
Electronegativity Series:
The Pauling electronegativity scale provides a numerical framework to compare electronegativity values across elements. This scale allows chemists to arrange elements in an electronegativity series, highlighting the varying degrees of electron attraction. The series aids in predicting molecular properties and chemical behaviour.
Importance of Electronegativity:
Electronegativity profoundly impacts various chemical phenomena:
Chemical Bonding:
Electronegativity determines the nature of chemical bonds, whether they are covalent, polar covalent, or ionic.
Reactivity:
Elements’ electronegativity drives their reactivity in chemical reactions, influencing their participation in electron transfers or bond formations.
Prediction of Properties:
The electronegativity series aids in predicting properties like boiling points, solubility, and acid-base behavior.
Conclusion:
Electronegativity provides a lens through which chemists interpret the behavior of elements and compounds. From the electronegativity series to predicting molecular structures and reactivity patterns, this concept is integral to understanding the language of chemistry. Whether exploring the diversity of elements on the periodic table or delving into the intricacies of molecular interactions, electronegativity guides scientists in deciphering the elegant dance of electrons that defines the world of chemistry.
Mapping Chemistry’s DNA: Exploring the Secrets of the Valency Chart
Introduction:
In the realm of chemistry, understanding the valency of elements is crucial for comprehending their behavior in chemical reactions and their participation in forming compounds. Valency charts serve as indispensable tools for visualizing and interpreting these valence interactions. This article delves into the significance of valency, the construction of a full valency chart encompassing all elements, and the invaluable insights provided by these charts.
Unravelling Valency:
Valency refers to the combining capacity of an element, indicating the number of electrons an atom gains, loses, or shares when forming chemical compounds. Valence electrons, occupying the outermost electron shell, are key players in these interactions, defining the chemical behaviour of an element.
Constructing a Full Valency Chart:
A full valency chart systematically presents the valence electrons of all elements, allowing chemists to predict the possible oxidation states and bonding patterns. The periodic table guides the organisation of this chart, categorising elements by their atomic number and electron configuration.
Benefits of Valency Charts:
Valency charts offer several advantages:
Predicting Compound Formation:
Valency charts facilitate predicting how elements interact and form compounds based on their valence electrons.
Balancing Chemical Equations:
Understanding valency helps in balancing chemical equations by ensuring the conservation of atoms and electrons.
Determining Oxidation States:
Valency charts assist in identifying the possible oxidation states of elements in compounds.
Classifying Elements:
Valency charts aid in classifying elements as metals, nonmetals, or metalloids based on their electron configuration.
Navigating the Valency Chart:
When using a valency chart, follow these steps:
Locate the Element:
Find the element in the chart based on its atomic number.
Identify Valence Electrons:
Observe the group number (column) to determine the number of valence electrons.
Predict Ionic Charges:
For main group elements, the valence electrons often dictate the ionic charge when forming ions.
Valency Chart and Periodic Trends:
Valency charts reflect periodic trends, such as the increase in valence electrons from left to right across a period and the tendency of main group elements to have a valency equal to their group number.
Conclusion:
Valency charts serve as compasses, guiding chemists through the intricate landscape of element interactions. By providing a visual representation of valence electrons and potential bonding patterns, these charts empower scientists to predict reactions, balance equations, and grasp the nuances of chemical behavior. In the pursuit of understanding the building blocks of matter, valency charts stand as essential tools, enabling us to navigate the complex world of chemistry with confidence and precision.
Unveiling the Latest Periodic Table of Elements: Exploring Structure, Uses, and Beyond
The periodic table of elements, a cornerstone of modern chemistry, has recently undergone intriguing updates. This table organizes the building blocks of matter, offering insight into the fundamental properties and behaviors of elements. It presents a symphony of elements, each characterized by atomic number, mass, and unique properties that hold the key to our understanding of the natural world.
Structure and Significance:
The latest periodic table boasts an elegant arrangement of elements based on atomic number, a value that defines the number of protons in an atom’s nucleus. This arrangement reflects the periodicity of elemental properties, with columns representing groups and rows signifying periods. As we traverse across a period, atomic numbers rise, unveiling new electron shells. Meanwhile, moving down a group introduces analogous valence electron configurations, leading to similar chemical behavior.
Atomic Number and Mass:
The atomic number, alongside atomic mass, is a cornerstone of the periodic table’s organization. The atomic mass of an element’s isotopes contributes to the weighted average that graces the table. Elements are classified as heavy or light based on this average, with the distinction often having profound implications for an element’s stability and reactivity.
Element Symbols and Uses:
Each element is denoted by a symbol derived from its name, often in Latin or its first few letters. These symbols provide a succinct way to represent elements and facilitate universal communication in the world of science.
The periodic table is more than just a collection of data; it holds practical significance. Elements find applications in countless industries and fields. Hydrogen, the lightest element, powers fuel cells and is crucial for the production of ammonia. Silicon, a cornerstone of electronics, underpins the modern digital age. Heavy elements, often forged in the heart of stars, play roles in nuclear reactors, medical imaging, and cutting-edge research.
Exploring Heavy Elements:
Heavy elements, found in the latter portions of the periodic table, captivate scientists and researchers. Many of these elements are synthesized in laboratories, often for fractions of a second, offering glimpses into uncharted territory. Elements like uranium and plutonium have far-reaching consequences in nuclear energy and weaponry, while newer, synthetic elements expand our understanding of the possible forms of matter.
Conclusion:
The periodic table of elements remains a testament to human curiosity and our ceaseless quest to understand the world around us. As we delve into the intricacies of atomic structure, properties, and applications, the periodic table’s latest iterations continue to serve as blueprints for innovation, guiding scientific discoveries that shape our present and future. The table’s rows and columns remind us of the interconnectedness of the elements and their profound influence on our lives, from the most mundane substances to the most advanced technological breakthroughs.
From Aromatics to Aldehydes: Mastering the Gattermann-Koch Transformation
Introduction:
Chemical transformations are the cornerstone of modern synthesis techniques, enabling the creation of diverse organic compounds. The Gattermann-Koch reaction, a formylation process, holds a significant place in the realm of organic chemistry. This article explores the mechanics of the Gattermann-Koch reaction, its formylation process, reagents involved, and exemplifies its application through real-world examples.
The Gattermann-Koch Reaction:
The Gattermann-Koch reaction is a method used for the synthesis of aldehydes from aromatic compounds. It allows the selective introduction of a formyl group (CHO) onto the aromatic ring, leading to the conversion of various aromatic compounds into aldehydes.
Mechanism of Gattermann-Koch Reaction:
The Gattermann-Koch reaction follows a two-step mechanism:
Formation of Diazonium Salt:
The aromatic compound reacts with hydrochloric acid (HCl) and sodium nitrite (NaNO2) to form a diazonium salt intermediate.
Formylation with Hydrogen Cyanide (HCN):
The diazonium salt is then treated with hydrogen cyanide (HCN), which is usually dissolved in the presence of copper(I) chloride (CuCl) or cuprous cyanide (CuCN). The reaction leads to the replacement of the diazonium group with a formyl group (-CHO), resulting in the formation of the aldehyde.
Reagents in Gattermann-Koch Reaction:
The key reagents involved in the Gattermann-Koch reaction are:
Sodium Nitrite (NaNO2):
Used to convert the aromatic compound into a diazonium salt.
Hydrogen Cyanide (HCN): Provides the formyl group for the formylation reaction.
Copper(I) Chloride (CuCl) or Cuprous Cyanide (CuCN):
Catalysts that facilitate the reaction between the diazonium salt and HCN.
Application and Examples:
The Gattermann-Koch reaction finds utility in the synthesis of various aromatic aldehydes. For example, the reaction can be used to convert benzene into benzaldehyde, or to formylate anisole to yield anisaldehyde. These aldehydes serve as versatile intermediates in the production of pharmaceuticals, fragrances, and specialty chemicals.
Conclusion:
The Gattermann-Koch reaction stands as a testament to the creativity and innovation within organic chemistry. By harnessing the power of reagents and reaction mechanisms, chemists can transform simple aromatic compounds into valuable aldehydes. From pharmaceuticals to flavoring agents, the aldehydes synthesized through this reaction have a broad range of applications that impact industries and improve our daily lives. As chemical understanding evolves, the Gattermann-Koch reaction continues to contribute to the expansion of the synthetic toolbox in the pursuit of novel compounds and groundbreaking discoveries.
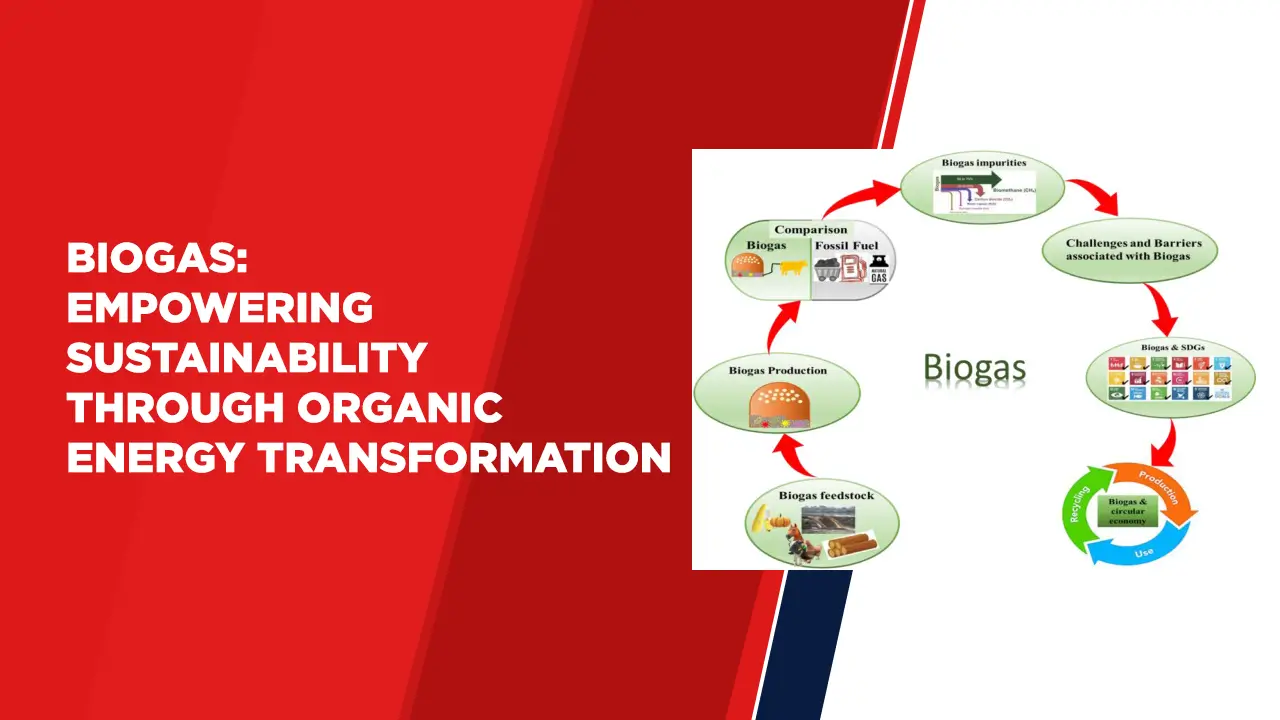
Biogas: Empowering Sustainability Through Organic Energy Transformation
Introduction:
In a time where the need for energy solutions and efficient organic waste management’s of utmost importance, biogas has emerged as a viable solution. Generated through digestion biogas is an energy source that not only tackles waste management problems but also helps in reducing greenhouse gas emissions. This article explores the mechanics of biogas production, its composition and the various ways it is revolutionizing the energy sector.
Understanding Biogas:
Biogas is a type of fuel that is created when microorganisms break down matter in an environment without oxygen. This natural process, called digestion, produces methane (CH4) and carbon dioxide (CO2) well, as small amounts of other gases. The specific composition of the gas can vary depending on the type of material being digested and the conditions under which it occurs.
Biogas Plant:
A biogas plant is a facility that is constructed with the intention of utilizing digestion to generate biogas. These plants create controlled conditions, for decomposing materials, like food waste, agricultural leftovers, sewage and animal manure. The generated biogas can be used for purposes making biogas plants contributors to waste management and the production of sustainable energy.
Biogas Production Process:
The production of biogas involves several stages:
Feedstock Collection:
Organic waste materials are collected and introduced into the biogas plant. These materials can include kitchen waste, crop residues, and even wastewater.
Anaerobic Digestion:
In the absence of oxygen, microorganisms break down the organic matter, releasing methane and carbon dioxide as byproducts.
Gas Collection:
The biogas produced is collected and stored, often in specially designed gas holders.
Purification:
To improve the quality of biogas and remove impurities, purification processes such as scrubbing or upgrading are employed.
Uses and Benefits of Biogas:
The applications of biogas extend across multiple sectors:
Energy Generation:
Biogas can be burned to produce heat or electricity, offering a renewable energy source that can be used for powering homes, industries, and even local power grids.
Cooking and Heating:
In rural and off-grid areas, biogas serves as a clean cooking fuel, replacing traditional biomass fuels that contribute to indoor air pollution.
Transportation:
Purified biogas, known as biomethane, can be used as a vehicle fuel, reducing carbon emissions in the transportation sector.
Waste Management:
By converting organic waste into biogas, the process mitigates landfill usage, reducing greenhouse gas emissions and tackling waste-related problems.
Composition and Environmental Impact:
The composition of biogas mainly consists of methane (CH4) and carbon dioxide (CO2) along with amounts of gases like hydrogen sulphide (H2S) and water vapor. The presence of methane is especially important as it contributes to the energy value of biogas. The. Use of biogas helps in reducing the release of methane, which is a powerful greenhouse gas, into the atmosphere.
Conclusion:
Biogas is a remarkable example of turning a waste issue into an energy and sustainability solution. Its ability to transform organic matter into a valuable fuel source underscores its significance in addressing waste management challenges and promoting renewable energy adoption. As we continue to explore avenues for reducing our carbon footprint and securing a cleaner future, biogas stands as a shining example of innovation, efficiency, and environmental responsibility.
English concepts:
English, with its vast vocabulary and roots in multiple languages, often leaves even native speakers grappling with correct pronunciations. Mispronunciations can stem from regional accents, linguistic influences, or simply the irregularities of English spelling. Here, we explore some commonly mispronounced words and provide tips to articulate them correctly.
1. Pronunciation
Common Mistake: Saying “pro-noun-ciation”
Correct: “pruh-nun-see-ay-shun”
This word ironically trips people up. Remember, it comes from the root “pronounce,” but the vowel sounds shift in “pronunciation.”
2. Mischievous
Common Mistake: Saying “mis-chee-vee-us”
Correct: “mis-chuh-vus”
This three-syllable word often gains an unnecessary extra syllable. Keep it simple!
3. Espresso
Common Mistake: Saying “ex-press-o”
Correct: “ess-press-o”
There is no “x” in this caffeinated delight. The pronunciation reflects its Italian origin.
4. February
Common Mistake: Saying “feb-yoo-air-ee”
Correct: “feb-roo-air-ee”
The first “r” is often dropped in casual speech, but pronouncing it correctly shows attention to detail.
5. Library
Common Mistake: Saying “lie-berry”
Correct: “lie-bruh-ree”
Avoid simplifying the word by dropping the second “r.” Practice enunciating all the syllables.
6. Nuclear
Common Mistake: Saying “nuke-yoo-lur”
Correct: “new-klee-ur”
This word, often heard in political discussions, has a straightforward two-syllable pronunciation.
7. Almond
Common Mistake: Saying “al-mond”
Correct: “ah-mund” (in American English) or “al-mund” (in British English)
Regional differences exist, but in American English, the “l” is typically silent.
8. Often
Common Mistake: Saying “off-ten”
Correct: “off-en”
Historically, the “t” was pronounced, but modern English favors the silent “t” in most accents.
9. Salmon
Common Mistake: Saying “sal-mon”
Correct: “sam-un”
The “l” in “salmon” is silent. Think of “salmon” as “sam-un.”
10. Et cetera
Common Mistake: Saying “ek-cetera”
Correct: “et set-er-uh”
Derived from Latin, this phrase means “and the rest.” Pronouncing it correctly can lend sophistication to your speech.
Tips to Avoid Mispronunciation:
- Listen and Repeat: Exposure to correct pronunciations through audiobooks, podcasts, or conversations with fluent speakers can help.
- Break It Down: Divide challenging words into syllables and practice saying each part.
- Use Online Resources: Websites like Forvo and dictionary apps often provide audio examples of words.
- Ask for Help: If unsure, don’t hesitate to ask someone knowledgeable or consult a reliable source.
Mastering the correct pronunciation of tricky words takes practice and patience, but doing so can significantly enhance your confidence and communication skills. Remember, every misstep is a stepping stone toward becoming more fluent!
Language learners and linguists alike rely on the International Phonetic Alphabet (IPA) as an essential tool to understand and master pronunciation. Developed in the late 19th century, the IPA provides a consistent system of symbols representing the sounds of spoken language. It bridges the gap between spelling and speech, offering clarity and precision in a world of linguistic diversity.
What is the IPA?
The IPA is a standardized set of symbols that represent each sound, or phoneme, of human speech. Unlike regular alphabets tied to specific languages, the IPA is universal, transcending linguistic boundaries. It encompasses vowels, consonants, suprasegmentals (like stress and intonation), and diacritics to convey subtle sound variations. For instance, the English word “cat” is transcribed as /kæt/, ensuring its pronunciation is clear to anyone familiar with the IPA, regardless of their native language.
Why is the IPA Important?
The IPA is invaluable in addressing the inconsistencies of English spelling. For example, consider the words “though,” “through,” and “tough.” Despite their similar spellings, their pronunciations—/\u03b8o\u028a/, /\u03b8ru\u02d0/, and /tʌf/—vary significantly. The IPA eliminates confusion by focusing solely on sounds, not spelling.
Additionally, the IPA is a cornerstone for teaching and learning pronunciation in foreign languages. By understanding the symbols, learners can accurately replicate sounds that do not exist in their native tongue. For instance, French nasal vowels or the German “/\u03c7/” sound can be practiced effectively using IPA transcriptions.
Applications of the IPA in Learning Pronunciation
- Consistency Across Languages: The IPA provides a consistent method for learning pronunciation, regardless of the language. For example, the symbol /\u0259/ represents the schwa sound in English, as in “sofa,” and also applies to other languages like French and German.
- Corrective Feedback: Teachers and learners can use the IPA to identify specific pronunciation errors. For instance, an English learner mispronouncing “think” as “sink” can see the difference between /\u03b8/ (voiceless dental fricative) and /s/ (voiceless alveolar fricative).
- Improved Listening Skills: Familiarity with the IPA sharpens listening comprehension. Recognizing sounds and their corresponding symbols trains learners to distinguish subtle differences, such as the distinction between /iː/ (“sheep”) and /\u026a/ (“ship”) in English.
- Self-Study Tool: Many dictionaries include IPA transcriptions, enabling learners to practice pronunciation independently. Online resources, such as Forvo and YouTube tutorials, often incorporate IPA to demonstrate sounds visually and audibly.
How to Learn the IPA
- Start Small: Begin with common sounds in your target language and gradually expand to more complex symbols.
- Use Visual Aids: IPA charts, available online, visually group sounds based on their articulation (e.g., plosives, fricatives, and vowels).
- Practice Regularly: Regular exposure to IPA transcriptions and practice with native speakers or recordings helps reinforce learning.
- Seek Professional Guidance: Enroll in language classes or consult linguists familiar with the IPA for advanced instruction.
Conclusion
The International Phonetic Alphabet is a powerful tool that simplifies the complex relationship between speech and writing. Its precision and universality make it an indispensable resource for language learners, educators, and linguists. By embracing the IPA, you can unlock the intricacies of pronunciation and enhance your ability to communicate effectively across languages.
English, as a global language, exhibits a remarkable diversity of accents that reflect the rich cultural and geographical contexts of its speakers. Regional accents not only shape the way English is pronounced but also contribute to the unique identity of communities. From the crisp enunciation of British Received Pronunciation (RP) to the melodic tones of Indian English, regional accents significantly influence how English sounds across the world.
What Are Regional Accents?
A regional accent is the distinct way in which people from a specific geographical area pronounce words. Factors like local dialects, historical influences, and contact with other languages contribute to the development of these accents. For instance, the Irish English accent retains traces of Gaelic phonetics, while American English shows influences from Spanish, French, and Indigenous languages.
Examples of Regional Accents in English
- British Accents:
- Received Pronunciation (RP): Often associated with formal British English, RP features clear enunciation and is commonly used in media and education.
- Cockney: This London-based accent drops the “h” sound (e.g., “house” becomes “‘ouse”) and uses glottal stops (e.g., “bottle” becomes “bo’le”).
- Scouse: Originating from Liverpool, this accent is characterized by its nasal tone and unique intonation patterns.
- American Accents:
- General American (GA): Considered a neutral accent in the U.S., GA lacks strong regional markers like “r-dropping” or vowel shifts.
- Southern Drawl: Found in the southern United States, this accent elongates vowels and has a slower speech rhythm.
- New York Accent: Known for its “r-dropping” (e.g., “car” becomes “cah”) and distinct pronunciation of vowels, like “coffee” pronounced as “caw-fee.”
- Global English Accents:
- Australian English: Features a unique vowel shift, where “day” may sound like “dye.”
- Indian English: Retains features from native languages, such as retroflex consonants and a syllable-timed rhythm.
- South African English: Combines elements of British English with Afrikaans influences, producing distinctive vowel sounds.
Impact of Regional Accents on Communication
- Intelligibility: While accents enrich language, they can sometimes pose challenges in global communication. For example, non-native speakers might struggle with understanding rapid speech or unfamiliar intonation patterns.
- Perceptions and Bias: Accents can influence how speakers are perceived, often unfairly. For instance, some accents are associated with prestige, while others may face stereotypes. Addressing these biases is crucial for fostering inclusivity.
- Cultural Identity: Accents serve as markers of cultural identity, allowing individuals to connect with their heritage. They also add color and diversity to the English language.
Embracing Accent Diversity
- Active Listening: Exposure to different accents through media, travel, or conversation helps improve understanding and appreciation of linguistic diversity.
- Pronunciation Guides: Resources like the International Phonetic Alphabet (IPA) can aid in recognizing and reproducing sounds from various accents.
- Celebrate Differences: Recognizing that there is no “correct” way to speak English encourages mutual respect and reduces linguistic prejudice.
Conclusion
Regional accents are a testament to the adaptability and richness of English as a global language. They highlight the influence of history, culture, and geography on pronunciation, making English a dynamic and evolving means of communication. By embracing and respecting these differences, we can better appreciate the beauty of linguistic diversity.
Speaking English with a foreign accent is a natural part of learning the language, as it reflects your linguistic background. However, some individuals may wish to reduce their accent to improve clarity or feel more confident in communication. Here are practical tips to help you minimize a foreign accent in English.
1. Listen Actively
One of the most effective ways to improve pronunciation is by listening to native speakers. Pay attention to how they pronounce words, their intonation, and rhythm. Watch movies, podcasts, or interviews in English and try to imitate the way speakers articulate words. Apps like YouTube or language learning platforms often provide valuable audio resources.
2. Learn the Sounds of English
English has a variety of sounds that may not exist in your native language. Familiarize yourself with these sounds using tools like the International Phonetic Alphabet (IPA). For example, practice distinguishing between similar sounds, such as /iː/ (“sheep”) and /\u026a/ (“ship”).
3. Practice with Minimal Pairs
Minimal pairs are words that differ by only one sound, such as “bat” and “pat” or “thin” and “tin.” Practicing these pairs can help you fine-tune your ability to hear and produce distinct English sounds.
4. Focus on Stress and Intonation
English is a stress-timed language, meaning certain syllables are emphasized more than others. Incorrect stress placement can make speech difficult to understand. For instance, “record” as a noun stresses the first syllable (RE-cord), while the verb stresses the second (re-CORD). Practice using the correct stress and pay attention to the natural rise and fall of sentences.
5. Slow Down and Enunciate
Speaking too quickly can amplify an accent and make it harder to pronounce words clearly. Slow down and focus on enunciating each syllable. Over time, clarity will become second nature, even at a normal speaking pace.
6. Use Pronunciation Apps and Tools
Modern technology offers numerous tools to help with pronunciation. Apps like Elsa Speak, Speechling, or even Google Translate’s audio feature can provide instant feedback on your speech. Use these tools to compare your pronunciation to that of native speakers.
7. Work with a Speech Coach or Tutor
A professional tutor can pinpoint areas where your pronunciation deviates from standard English and provide targeted exercises to address them. Many language tutors specialize in accent reduction and can help accelerate your progress.
8. Record Yourself
Hearing your own voice is a powerful way to identify areas for improvement. Record yourself reading passages or practicing conversations, then compare your speech to native speakers’ recordings.
9. Practice Daily
Consistency is key to reducing an accent. Dedicate time each day to practicing pronunciation. Whether through speaking, listening, or shadowing (repeating immediately after a speaker), regular practice builds muscle memory for English sounds.
10. Be Patient and Persistent
Reducing an accent is a gradual process that requires dedication. Celebrate small improvements and focus on becoming more comprehensible rather than achieving perfection.
Conclusion
While a foreign accent is part of your linguistic identity, reducing it can help you communicate more effectively in English. By actively listening, practicing consistently, and using available tools and resources, you can achieve noticeable improvements in your pronunciation. Remember, the goal is clarity and confidence, not eliminating your unique voice.
Clear pronunciation is a cornerstone of effective communication. While vocabulary and grammar are essential, the physical aspects of speech production, particularly mouth and tongue positioning, play a critical role in producing accurate sounds. Understanding and practicing proper articulation techniques can significantly enhance clarity and confidence in speech.
How Speech Sounds Are Produced
Speech sounds are created by the interaction of various speech organs, including the lips, tongue, teeth, and vocal cords. The tongue’s positioning and movement, combined with the shape of the mouth, determine the quality and accuracy of sounds. For example, vowels are shaped by the tongue’s height and position in the mouth, while consonants involve specific points of contact between the tongue and other parts of the oral cavity.
The Role of the Tongue
- Vowel Sounds:
- The tongue’s position is critical in forming vowels. For instance, high vowels like /iː/ (“beat”) require the tongue to be raised close to the roof of the mouth, while low vowels like /\u00e6/ (“bat”) require the tongue to be positioned lower.
- Front vowels, such as /e/ (“bet”), are produced when the tongue is closer to the front of the mouth, whereas back vowels like /uː/ (“boot”) involve the tongue retracting toward the back.
- Consonant Sounds:
- The tongue’s precise placement is crucial for consonants. For example, the /t/ and /d/ sounds are formed by the tongue touching the alveolar ridge (the ridge behind the upper teeth), while the /k/ and /g/ sounds are made with the back of the tongue against the soft palate.
- Sounds like /\u0283/ (“sh” as in “she”) require the tongue to be slightly raised and positioned near the hard palate without touching it.
The Role of the Mouth
- Lip Movement:
- Rounded vowels like /oʊ/ (“go”) involve the lips forming a circular shape, while unrounded vowels like /\u0251ː/ (“father”) keep the lips relaxed.
- Labial consonants, such as /p/, /b/, and /m/, rely on the lips coming together or closing.
- Jaw Position:
- The jaw’s openness affects the production of sounds. For example, open vowels like /\u0251ː/ require a wider jaw opening compared to close vowels like /iː/.
Improving Pronunciation Through Positioning
- Mirror Practice: Observe your mouth and tongue movements in a mirror while speaking. This visual feedback can help you make necessary adjustments.
- Phonetic Exercises: Practice individual sounds by focusing on the tongue and mouth’s required positions. For instance, repeat minimal pairs like “ship” and “sheep” to differentiate between /\u026a/ and /iː/.
- Use Pronunciation Guides: Resources like the International Phonetic Alphabet (IPA) provide detailed instructions on mouth and tongue positioning for each sound.
- Seek Feedback: Work with a language coach or use pronunciation apps that provide real-time feedback on your articulation.
Common Challenges and Solutions
- Retroflex Sounds: Some learners struggle with retroflex sounds, where the tongue curls back slightly. Practicing these sounds slowly and with guidance can improve accuracy.
- Th Sounds (/\u03b8/ and /\u00f0/): Non-native speakers often find it challenging to position the tongue between the teeth for these sounds. Practice holding the tongue lightly between the teeth and exhaling.
- Consistency: Regular practice is essential. Even small daily efforts can lead to noticeable improvements over time.
Conclusion
Clear pronunciation is not merely about knowing the right words but also mastering the physical aspects of speech. Proper mouth and tongue positioning can significantly enhance your ability to articulate sounds accurately and communicate effectively. By focusing on these elements and practicing consistently, you can achieve greater clarity and confidence in your speech.
Geography concepts:
The Earth, a dynamic and complex planet, has a layered structure that plays a crucial role in shaping its physical characteristics and geological processes. These layers are distinguished based on their composition, state, and physical properties. Understanding the Earth’s structure is fundamental for studying phenomena such as earthquakes, volcanism, and plate tectonics.
The Earth’s Layers
The Earth is composed of three main layers: the crust, the mantle, and the core. Each layer is unique in its composition and function.
1. The Crust
The crust is the outermost and thinnest layer of the Earth. It is divided into two types:
- Continental Crust: Thicker (30-70 km), less dense, and composed mainly of granite.
- Oceanic Crust: Thinner (5-10 km), denser, and primarily composed of basalt.
The crust forms the Earth’s surface, including continents and ocean floors. It is broken into tectonic plates that float on the underlying mantle.
2. The Mantle
Beneath the crust lies the mantle, which extends to a depth of about 2,900 km. It constitutes about 84% of the Earth’s volume. The mantle is primarily composed of silicate minerals rich in iron and magnesium.
The mantle is subdivided into:
- Upper Mantle: Includes the lithosphere (rigid outer part) and the asthenosphere (semi-fluid layer that allows plate movement).
- Lower Mantle: More rigid due to increased pressure but capable of slow flow.
Convection currents in the mantle drive the movement of tectonic plates, leading to geological activity like earthquakes and volcanic eruptions.
3. The Core
The core, the innermost layer, is divided into two parts:
- Outer Core: A liquid layer composed mainly of iron and nickel. It extends from 2,900 km to 5,150 km below the surface. The movement of the liquid outer core generates the Earth’s magnetic field.
- Inner Core: A solid sphere made primarily of iron and nickel, with a radius of about 1,220 km. Despite the extreme temperatures, the inner core remains solid due to immense pressure.
Transition Zones
The boundaries between these layers are marked by distinct changes in seismic wave velocities:
- Mohorovičić Discontinuity (Moho): The boundary between the crust and the mantle.
- Gutenberg Discontinuity: The boundary between the mantle and the outer core.
- Lehmann Discontinuity: The boundary between the outer core and the inner core.
Significance of the Earth’s Structure
- Seismic Studies: The study of seismic waves helps scientists understand the Earth’s internal structure and composition.
- Plate Tectonics: Knowledge of the lithosphere and asthenosphere explains plate movements and related phenomena like earthquakes and mountain building.
- Magnetic Field: The outer core’s dynamics are crucial for generating the Earth’s magnetic field, which protects the planet from harmful solar radiation.
Earthquakes, one of the most striking natural phenomena, release energy in the form of seismic waves that travel through the Earth. The study of these waves is vital to understanding the internal structure of our planet and assessing the impacts of seismic activity. Earthquake waves, classified into body waves and surface waves, exhibit distinct characteristics and behaviors as they propagate through different layers of the Earth.
Body Waves
Body waves travel through the Earth’s interior and are of two main types: primary waves (P-waves) and secondary waves (S-waves).
P-Waves (Primary Waves)
- Characteristics: P-waves are compressional or longitudinal waves, causing particles in the material they pass through to vibrate in the same direction as the wave’s movement.
- Speed: They are the fastest seismic waves, traveling at speeds of 5-8 km/s in the Earth’s crust and even faster in denser materials.
- Medium: P-waves can travel through solids, liquids, and gases, making them the first waves to be detected by seismographs during an earthquake.
S-Waves (Secondary Waves)
- Characteristics: S-waves are shear or transverse waves, causing particles to move perpendicular to the wave’s direction of travel.
- Speed: They are slower than P-waves, traveling at about 3-4 km/s in the Earth’s crust.
- Medium: S-waves can only move through solids, as liquids and gases do not support shear stress.
- Significance: The inability of S-waves to pass through the Earth’s outer core provides evidence of its liquid nature.
Surface Waves
Surface waves travel along the Earth’s crust and are slower than body waves. However, they often cause the most damage during earthquakes due to their high amplitude and prolonged shaking. There are two main types of surface waves: Love waves and Rayleigh waves.
Love Waves
- Characteristics: Love waves cause horizontal shearing of the ground, moving the surface side-to-side.
- Impact: They are highly destructive to buildings and infrastructure due to their horizontal motion.
Rayleigh Waves
- Characteristics: Rayleigh waves generate a rolling motion, combining both vertical and horizontal ground movement.
- Appearance: Their motion resembles ocean waves and can be felt at greater distances from the earthquake’s epicenter.
Propagation Through the Earth
The behavior of earthquake waves provides invaluable information about the Earth’s internal structure:
- Reflection and Refraction: As seismic waves encounter boundaries between different materials, such as the crust and mantle, they reflect or refract, altering their speed and direction.
- Shadow Zones: P-waves and S-waves create shadow zones—regions on the Earth’s surface where seismic waves are not detected—offering clues about the composition and state of the Earth’s interior.
- Wave Speed Variations: Changes in wave velocity reveal differences in density and elasticity of the Earth’s layers.
Sea floor spreading is a fundamental process in plate tectonics that explains the formation of a new oceanic crust and the dynamic nature of Earth’s lithosphere. First proposed by Harry Hess in the early 1960s, this concept revolutionized our understanding of ocean basins and their role in shaping Earth’s geological features.
What is Sea Floor Spreading?
Sea floor spreading occurs at mid-ocean ridges, which are underwater mountain ranges that form along divergent plate boundaries. At these ridges, magma rises from the mantle, cools, and solidifies to create a new oceanic crust. As this new crust forms, it pushes the older crust away from the ridge, causing the ocean floor to expand.
This continuous process is driven by convection currents in the mantle, which transport heat and material from Earth’s interior to its surface.
Key Features of Sea Floor Spreading
- Mid-Ocean Ridges: These are the sites where sea floor spreading begins. Examples include the Mid-Atlantic Ridge and the East Pacific Rise. These ridges are characterized by volcanic activity and high heat flow.
- Magnetic Striping: As magma solidifies at mid-ocean ridges, iron-rich minerals within it align with Earth’s magnetic field. Over time, the magnetic field reverses, creating alternating magnetic stripes on either side of the ridge. These stripes serve as a record of Earth’s magnetic history and provide evidence for sea floor spreading.
- Age of the Ocean Floor: The age of the oceanic crust increases with distance from the mid-ocean ridge. The youngest rocks are found at the ridge, while the oldest rocks are located near subduction zones where the oceanic crust is recycled back into the mantle.
Evidence Supporting Sea Floor Spreading
Magnetic Anomalies: The symmetrical pattern of magnetic stripes on either side of mid-ocean ridges corresponds to Earth’s magnetic reversals, confirming the creation and movement of oceanic crust.
Seafloor Topography: The discovery of mid-ocean ridges and deep-sea trenches provided physical evidence for the process of spreading and subduction.
Ocean Drilling: Samples collected from the ocean floor show that sediment thickness and crust age increases with distance from mid-ocean ridges, supporting the idea of continuous crust formation and movement.
Heat Flow Measurements: Elevated heat flow near mid-ocean ridges indicates active magma upwelling and crust formation.
Role in Plate Tectonics
Sea floor spreading is integral to the theory of plate tectonics, as it explains the movement of oceanic plates. The process creates new crust at divergent boundaries and drives plate motion, leading to interactions at convergent boundaries (subduction zones) and transform boundaries (faults).
Impact on Earth’s Geology
Creation of Ocean Basins: Sea floor spreading shapes the structure of ocean basins, influencing global geography over millions of years.
Earthquakes and Volcanism: The process generates earthquakes and volcanic activity at mid-ocean ridges and subduction zones.
Continental Drift: Sea floor spreading provides a mechanism for continental drift, explaining how continents move apart over time.
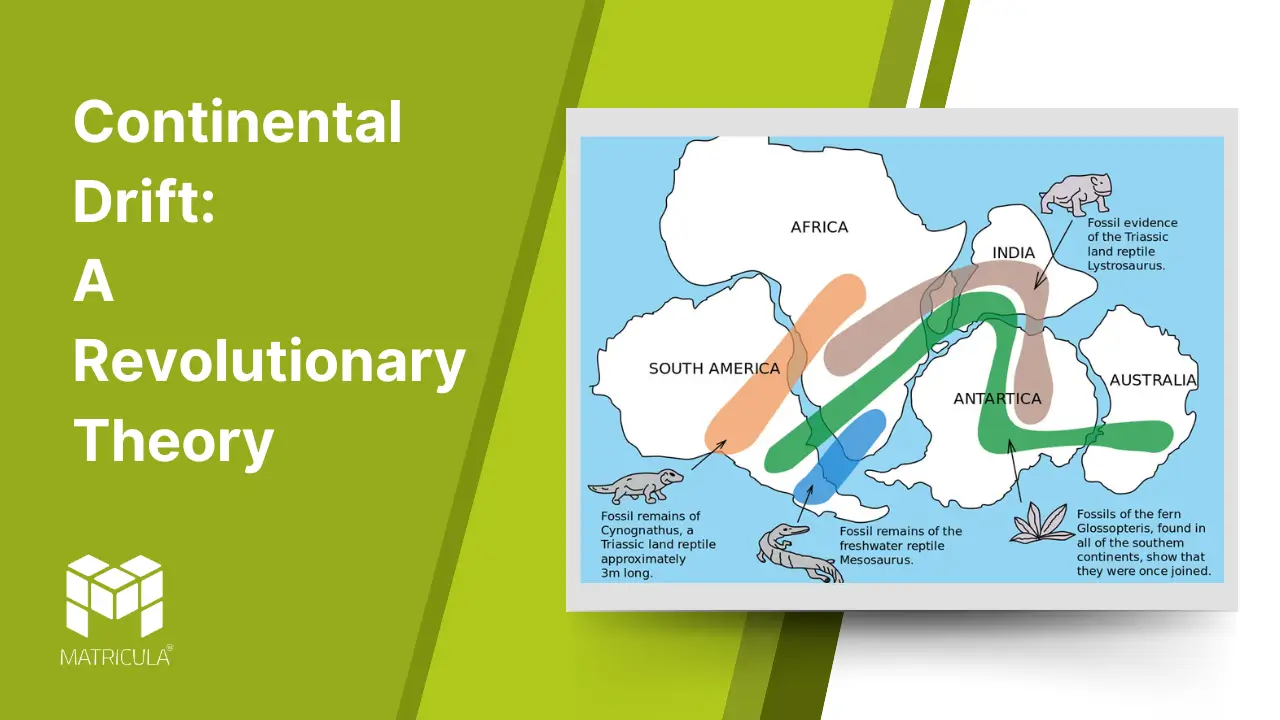
Continental drift is a scientific theory that revolutionized our understanding of Earth’s geography and geological processes. Proposed by German meteorologist and geophysicist Alfred Wegener in 1912, the theory posits that continents were once joined together in a single landmass and have since drifted apart over geological time.
The Origin of Continental Drift Theory
Alfred Wegener introduced the idea of a supercontinent called Pangaea, which existed around 300 million years ago. Over time, this landmass fragmented and its pieces drifted to their current positions. Wegener’s theory challenged the prevailing notion that continents and oceans had remained fixed since the Earth’s formation.
Evidence Supporting Continental Drift
Fit of the Continents: The coastlines of continents like South America and Africa fit together like puzzle pieces, suggesting they were once joined.
Fossil Evidence: Identical fossils of plants and animals, such as Mesosaurus (a freshwater reptile), have been found on continents now separated by oceans. This indicates that these continents were once connected.
Geological Similarities: Mountain ranges, such as the Appalachian Mountains in North America and the Caledonian Mountains in Europe, share similar rock compositions and structures, hinting at a shared origin.
Paleoclimatic Evidence: Evidence of glaciation, such as glacial striations, has been found in regions that are now tropical, like India and Africa, suggesting these regions were once closer to the poles.
Challenges to Wegener’s Theory
Despite its compelling evidence, Wegener’s theory faced criticism because he could not explain the mechanism driving the continents’ movement. At the time, the scientific community lacked knowledge about the Earth’s mantle and plate tectonics, which are now understood to be key to continental movement.
Link to Plate Tectonics
The theory of plate tectonics, developed in the mid-20th century, provided the missing mechanism for continental drift. It describes the Earth’s lithosphere as divided into tectonic plates that float on the semi-fluid asthenosphere beneath them. Convection currents in the mantle drive the movement of these plates, causing continents to drift, collide, or separate.
Impact of Continental Drift
- Formation of Landforms: The drifting of continents leads to the creation of mountain ranges, ocean basins, and rift valleys.
- Earthquakes and Volcanoes: The interaction of tectonic plates at their boundaries results in seismic and volcanic activity.
- Biogeography: The movement of continents explains the distribution of species and the evolution of unique ecosystems.
The Earth’s surface, dynamic and ever-changing, is shaped by powerful forces operating beneath the crust. Among the key theories explaining these processes are Alfred Wegener’s Continental Drift Theory and the modern understanding of Plate Tectonics. These concepts are fundamental to understanding earthquakes and volcanoes, two of the most dramatic natural phenomena.
Wegener’s Continental Drift Theory
In 1912, Alfred Wegener proposed the Continental Drift Theory, suggesting that the continents were once joined together in a single supercontinent called “Pangaea.” Over millions of years, Pangaea fragmented, and the continents drifted to their current positions.
Wegener supported his hypothesis with several lines of evidence:
- Fossil Correlation: Identical fossils of plants and animals, such as Mesosaurus and Glossopteris, were found on continents now separated by oceans.
- Geological Similarities: Mountain ranges and rock formations on different continents matched perfectly, such as the Appalachian Mountains in North America aligning with mountain ranges in Scotland.
- Climate Evidence: Glacial deposits in regions now tropical and coal deposits in cold areas suggested significant shifts in continental positioning.
Despite its compelling evidence, Wegener’s theory was not widely accepted during his lifetime due to the lack of a mechanism explaining how continents moved.
Plate Tectonics: The Modern Perspective
The theory of Plate Tectonics, developed in the mid-20th century, provided the mechanism that Wegener’s theory lacked. The Earth’s lithosphere is divided into large, rigid plates that float on the semi-fluid asthenosphere beneath. These plates move due to convection currents in the mantle, caused by heat from the Earth’s core.
Plate Boundaries
Divergent Boundaries: Plates move apart, forming new crust as magma rises to the surface. Example: The Mid-Atlantic Ridge.
Convergent Boundaries: Plates collide, leading to subduction (one plate sinking beneath another) or the formation of mountain ranges. Example: The Himalayas.
Transform Boundaries: Plates slide past each other horizontally, causing earthquakes. Example: The San Andreas Fault.
Earthquakes
Earthquakes occur when stress builds up along plate boundaries and is suddenly released, causing the ground to shake. They are measured using the Richter scale or the moment magnitude scale, and their epicenters and depths are crucial to understanding their impacts.
Types of Earthquakes
Tectonic Earthquakes: Caused by plate movements at boundaries.
Volcanic Earthquakes: Triggered by volcanic activity.
Human-Induced Earthquakes: Resulting from mining, reservoir-induced seismicity, or other human activities.
Volcanoes
Volcanoes are formed when magma from the Earth’s mantle reaches the surface. Their occurrence is closely linked to plate boundaries:
Subduction Zones: As one plate subducts, it melts and forms magma, leading to volcanic eruptions. Example: The Pacific Ring of Fire.
Divergent Boundaries: Magma emerges where plates pull apart, as seen in Iceland.
Hotspots: Volcanoes form over mantle plumes, independent of plate boundaries. Example: Hawaii.
Types of Volcanoes
Shield Volcanoes: Broad and gently sloping, with non-explosive eruptions.
Composite Volcanoes: Steep-sided and explosive, formed by alternating layers of lava and ash.
Cinder Cone Volcanoes: Small, steep, and composed of volcanic debris.
History concepts:
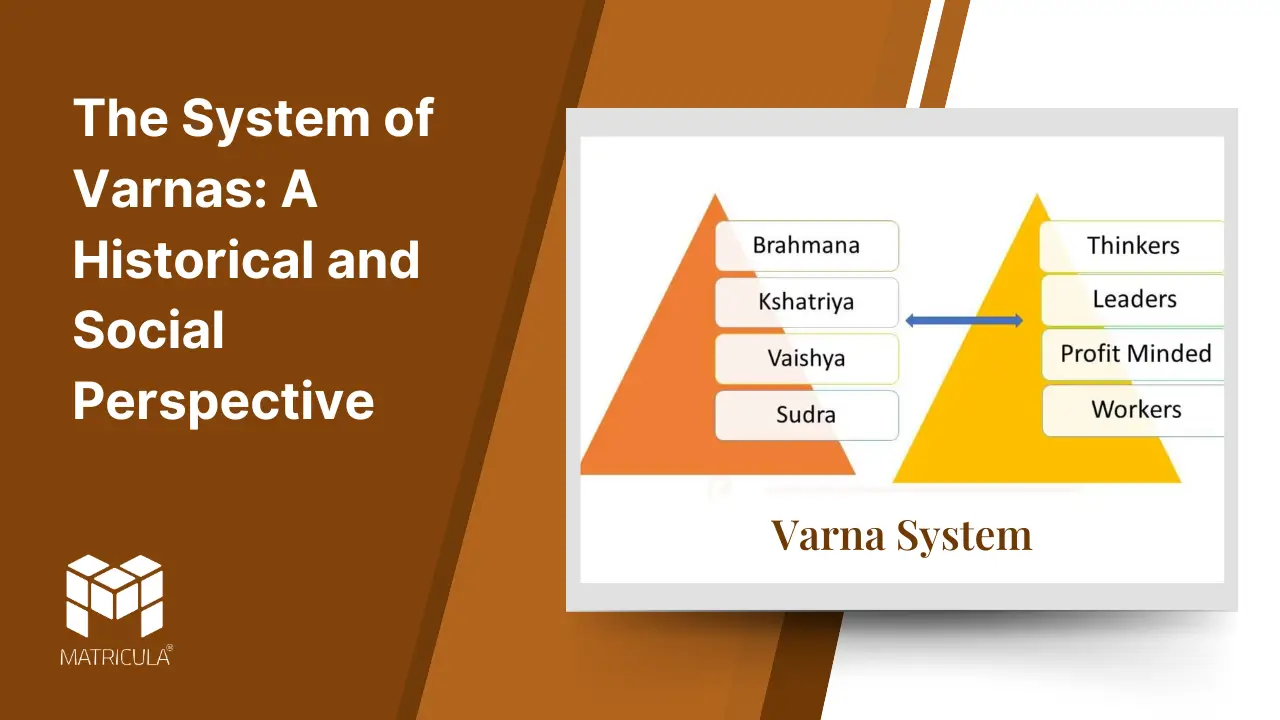
The system of varnas, central to ancient Indian society, is a framework of social stratification described in Hindu scriptures. Derived from the Sanskrit word varna, meaning “color” or “type,” this system categorized society into four broad groups based on occupation and duty (dharma). While initially envisioned as a functional and fluid classification, the varna system evolved into a rigid social hierarchy over time, shaping the social, economic, and cultural dynamics of the Indian subcontinent.
Origins and Structure of the Varna System
The earliest mention of the varna system is found in the Rigveda, one of Hinduism’s oldest texts, in a hymn known as the Purusha Sukta. This hymn describes society as emerging from the cosmic being (Purusha), with each varna symbolizing a part of the divine body:
- Brahmins (priests and scholars) were associated with the head, symbolizing wisdom and intellectual pursuits. They were tasked with preserving sacred knowledge, performing rituals, and providing spiritual guidance.
- Kshatriyas (warriors and rulers) were linked to the arms, representing strength and governance. They were responsible for protecting society and upholding justice.
- Vaishyas (merchants and agriculturists) were associated with the thighs, signifying sustenance and trade. They contributed to the economy through commerce, farming, and animal husbandry.
- Shudras (laborers and service providers) were connected to the feet, symbolizing support and service. They were tasked with manual labor and serving the other three varnas.
This division was rooted in the principle of dharma, with each varna fulfilling specific societal roles for the collective well-being.
Evolution into a Caste System
Initially, the varna system was fluid, allowing individuals to shift roles based on their abilities and actions. However, over time, it became closely linked to birth, giving rise to the rigid caste system (jati). This shift entrenched social hierarchies, limiting mobility and creating a stratified society.
The caste system introduced numerous sub-castes and emphasized endogamy (marrying within the same caste), further solidifying divisions. Those outside the varna system, often referred to as “Dalits” or “untouchables,” faced severe discrimination, as they were deemed impure and relegated to marginalized roles.
Impact and Criticism
The varna system profoundly influenced Indian society, dictating access to education, wealth, and power. While it provided a framework for social organization, it also perpetuated inequality and exclusion.
Reformers and thinkers like Buddha, Mahavira, and later figures like Mahatma Gandhi criticized the rigidity and discrimination inherent in the caste system. Gandhi referred to Dalits as Harijans (“children of God”) and worked to integrate them into mainstream society. In modern India, constitutional measures and affirmative action aim to address caste-based discrimination.
Varna in Contemporary Context
Today, the varna system’s relevance has diminished, but its legacy persists in the form of caste-based identities. Social and political movements in India continue to grapple with the enduring effects of caste hierarchies, striving to create a more equitable society.
In the annals of history, few individuals have demonstrated the intellectual curiosity and openness to other cultures as vividly as Al-Biruni. A Persian polymath born in 973 CE, Al-Biruni is celebrated for his pioneering contributions to fields such as astronomy, mathematics, geography, and anthropology. Among his most remarkable achievements is his systematic study of India, captured in his seminal work, Kitab al-Hind (The Book of India). This text is a testament to Al-Biruni’s efforts to make sense of a culture and tradition vastly different from his own—what he referred to as the “Sanskritic tradition.”
Encountering an “Alien World”
Al-Biruni’s journey to India was a consequence of the conquests of Mahmud of Ghazni, whose campaigns brought the scholar into contact with the Indian subcontinent. Rather than viewing India solely through the lens of conquest, Al-Biruni sought to understand its intellectual and cultural heritage. His approach was one of immersion: he studied Sanskrit, the classical language of Indian scholarship, and engaged deeply with Indian texts and traditions.
This effort marked Al-Biruni as a unique figure in the cross-cultural exchanges of his time. Where others may have dismissed or misunderstood India’s complex systems of thought, he sought to comprehend them on their own terms, recognizing the intrinsic value of Indian philosophy, science, and spirituality.
Decoding the Sanskritic Tradition
The Sanskritic tradition, encompassing India’s rich repository of texts in philosophy, religion, astronomy, and mathematics, was largely inaccessible to outsiders due to its linguistic and cultural complexity. Al-Biruni overcame these barriers by studying key Sanskrit texts like the Brahmasphutasiddhanta of Brahmagupta, a seminal work on astronomy and mathematics.
In Kitab al-Hind, Al-Biruni systematically analyzed Indian cosmology, religious practices, and societal norms. He compared Indian astronomy with the Ptolemaic system prevalent in the Islamic world, highlighting areas of convergence and divergence. He also explored the philosophical underpinnings of Indian religions such as Hinduism, Buddhism, and Jainism, offering detailed accounts of their doctrines, rituals, and scriptures.
What set Al-Biruni apart was his objectivity. Unlike many medieval accounts, his descriptions avoided denigration or stereotyping. He acknowledged the strengths and weaknesses of Indian thought without imposing his own cultural biases, striving for an intellectual honesty that remains a model for cross-cultural understanding.
Bridging Cultures Through Scholarship
Al-Biruni’s work was not merely an intellectual exercise but a bridge between civilizations. By translating and explaining Indian ideas in terms familiar to Islamic scholars, he facilitated a dialogue between two great intellectual traditions. His observations introduced the Islamic world to Indian advances in mathematics, including concepts of zero and decimal notation, which would later influence global scientific progress.
Moreover, his nuanced portrayal of Indian culture countered the simplistic narratives of foreign conquest, offering a more empathetic and respectful view of a complex society.
Legacy and Relevance
Al-Biruni’s approach to the Sanskritic tradition underscores the timeless value of intellectual curiosity, humility, and cultural exchange. His work demonstrates that understanding an “alien world” requires not just knowledge but also respect for its inherent logic and values. In a world increasingly defined by globalization, his legacy offers a compelling blueprint for navigating cultural diversity with insight and empathy.
Al-Biruni remains a shining example of how scholarship can transcend the boundaries of language, religion, and geography, enriching humanity’s collective understanding of itself.
François Bernier, a French physician and traveler from the 17th century, is often remembered not only for his medical expertise but also for his distinctive approach to anthropology and his contribution to the understanding of race and society. His unique career and pioneering thoughts have left an indelible mark on both medical history and social science.
Early Life and Education
Born in 1625 in the small town of Bergerac in southwestern France, François Bernier was initially drawn to the medical field. He studied at the University of Montpellier, one of the most renowned medical schools of the time, where he earned his degree in medicine. However, it was not just the practice of medicine that fascinated Bernier; his intellectual curiosity stretched far beyond the confines of the classroom, drawing him to explore various cultures and societies across the world.
A Journey Beyond Medicine
In 1653, Bernier left France for the Mughal Empire, one of the most powerful and culturally rich regions of the time, as a personal physician to the Mughal emperor’s court. His experiences in India greatly influenced his thinking and the trajectory of his career. During his time in the subcontinent, Bernier not only treated the emperor’s court but also observed the vast cultural and racial diversity within the empire.
His observations were not just medical but also social and anthropological, laying the foundation for his most famous work, Travels in the Mughal Empire. In his book, Bernier provided a detailed account of the Mughal Empire’s political structure, the customs of its people, and the unique geography of the region. However, it was his discussions on race and human classification that were most groundbreaking.
Bernier’s View on Race
François Bernier’s thoughts on race were far ahead of his time. In a work published in 1684, Nouvelle Division de la Terre par les Différentes Especes ou Races qui l’Habitent (A New Division of the Earth by the Different Species or Races that Inhabit It), Bernier proposed a classification of humans based on physical characteristics, which is considered one of the earliest attempts at racial categorization in scientific discourse.
Bernier divided humanity into four major “races,” a concept he introduced to explain the differences he observed in people across different parts of the world. These included the Europeans, the Africans, the Asians, and the “Tartars” or people from the Mongol region. While his ideas on race are considered outdated and problematic today, they were groundbreaking for their time and laid the groundwork for later anthropological and racial theories.
Legacy and Influence
Bernier’s contributions went beyond the realm of medicine and anthropology. His writings were influential in European intellectual circles and contributed to the growing European interest in the non-Western world. His observations, especially regarding the Indian subcontinent, provided European readers with a new understanding of distant lands and cultures. In the context of medical history, his role as a physician in the Mughal court also underscores the importance of medical exchanges across different cultures during the 17th century.
François Bernier died in 1688, but his legacy continued to shape the fields of medicine, anthropology, and colonial studies long after his death. Although his views on race would be critically examined and challenged in the centuries to follow, his adventurous spirit and intellectual curiosity left an indelible mark on the study of human diversity and the interconnectedness of the world.
Ibn Battuta, a name synonymous with one of the most remarkable travel accounts in history, was a Moroccan scholar and explorer who ventured across the Islamic world and beyond during the 14th century. His journey, recorded in the famous book Rihla (which means “The Journey”), offers a detailed narrative of his travels, spanning nearly 30 years and covering over 120,000 kilometers across Africa, the Middle East, Central Asia, India, Southeast Asia, and China.
The Beginnings of the Journey
Ibn Battuta was born in 1304 in Tangier, Morocco. At the age of 21, he set off on his pilgrimage to Mecca, a journey known as the Hajj, which was a significant spiritual and religious undertaking for a Muslim in the medieval era. However, his journey did not end in Mecca. Ibn Battuta was fascinated by the world beyond his homeland and the opportunities to explore foreign lands. What began as a religious journey evolved into an extensive exploration of cultures, societies, and landscapes far beyond the reach of most medieval travelers.
The Scope of Ibn Battuta’s Travels
Ibn Battuta’s travels spanned three continents and took him to some of the most influential and diverse regions of the time. His Rihla describes his experiences in places like Egypt, Persia, India, Sri Lanka, the Maldives, and China. One of the most remarkable aspects of his journey was his deep interaction with different cultures. He didn’t merely visit cities; he embedded himself in the societies he encountered, often serving as a judge, advisor, or diplomat in various courts.
In India, for example, Ibn Battuta served as a qadi (judge) in the court of the Sultan of Delhi, Muhammad bin Tughlaq, and wrote extensively about the culture, politics, and the complexities of the Indian subcontinent. He was particularly struck by the wealth and diversity of the region, noting the intricate systems of governance and the vibrant trade routes.
His travels in China, then under the rule of the Yuan Dynasty, were also significant. He was one of the few explorers of his time to document the far-reaching influence of China’s empire, including its advanced technological innovations like paper money and gunpowder.
The Significance of the Rihla
The Rihla was originally dictated to a scholar named Ibn Juzay, who compiled the narratives into a cohesive travelogue. The text offers unique insights into the medieval world from a Muslim perspective, chronicling the cities, people, customs, and practices that Ibn Battuta encountered. Beyond the traveler’s personal experiences, the Rihla provides historical and geographical knowledge, contributing to the understanding of the political dynamics of various regions during the 14th century.
Ibn Battuta’s Rihla is not only a travelogue but also a document of cultural exchange, religious thought, and the challenges of long-distance travel during the medieval period. It serves as a reminder of the medieval world’s interconnectedness, showing how the exchange of ideas, trade, and culture transcended geographical boundaries.
The social fabric of historical societies often reflects the complex interplay of power, gender, and labor. In this context, the lives of women slaves, the practice of Sati, and the conditions of laborers serve as poignant examples of systemic inequalities and cultural practices that shaped historical societies, particularly in the Indian subcontinent and beyond.
Women Slaves: Instruments of Power and Oppression
Women slaves were a significant part of ancient and medieval societies, valued not only for their labor but also for their perceived role in reinforcing the power of their masters. In ancient India, women slaves often served in royal households, working as domestic servants, concubines, or entertainers. Their lives were marked by a lack of autonomy, with their fates tied to the whims of their owners.
During the Delhi Sultanate and Mughal periods, the slave trade flourished, and women slaves were commonly brought from Central Asia, Africa, and neighboring regions. These women were sometimes educated and trained in music, dance, or languages to serve as courtesans or companions in elite households. While some gained influence due to proximity to power, most lived under harsh conditions, stripped of their freedom and dignity.
The plight of women slaves highlights the gendered nature of oppression, where women’s labor and bodies were commodified in systems of power and control.
Sati: A Controversial Practice of Widow Immolation
Sati, the practice of a widow immolating herself on her husband’s funeral pyre, is one of the most debated and controversial aspects of Indian history. Though not universally practiced, it became a powerful symbol of female sacrifice and devotion in certain regions and communities.
Rooted in patriarchal notions of honor and purity, sati was often glorified in medieval texts and inscriptions. However, historical evidence suggests that social and familial pressures played a significant role in coercing widows into this act. It was not merely a personal choice but a reflection of societal expectations and the lack of agency afforded to women, particularly widows who were seen as burdens on their families.
Colonial administrators like the British outlawed sati in the 19th century, with notable Indian reformers like Raja Ram Mohan Roy advocating for its abolition. The practice, though rare, became a rallying point for early feminist movements in India.
Labourers: The Backbone of Society
Laborers, both men and women, have historically constituted the backbone of agrarian and industrial societies. In India, the majority of laborers belonged to lower castes or tribal communities, often subjected to exploitative practices like bonded labor. Women laborers, in particular, faced double exploitation: as members of marginalized communities and as women subjected to gender discrimination.
Women laborers worked in fields, construction sites, and domestic settings, often earning meager wages and enduring harsh working conditions. Despite their significant contributions to the economy, their labor was undervalued, and their rights remained unrecognized for centuries.
Legacy and Modern Reflections
The historical realities of women slaves, sati, and laborers underscore the deeply entrenched inequalities in traditional societies. While these practices and systems have evolved or disappeared over time, their echoes remain in contemporary struggles for gender equality, labor rights, and social justice.
Efforts to address these historical injustices continue through legal reforms, social movements, and education, aiming to build a more equitable society. Understanding these past realities is essential for shaping a future free of oppression and exploitation.
Maths concepts:
Prime numbers are among the most intriguing and essential concepts in mathematics. Often referred to as the “building blocks” of numbers, primes are integers greater than 1 that have no divisors other than 1 and themselves. Their simplicity belies their profound importance in fields ranging from number theory to cryptography and computer science.
What Are Prime Numbers?
A prime number is defined as a natural number greater than 1 that cannot be divided evenly by any number other than 1 and itself. For example, 2,3,5,7,11,13,… are prime numbers. Numbers that are not prime are called composite numbers because they can be expressed as a product of smaller natural numbers.
Characteristics of Prime Numbers
Uniqueness:
- Prime numbers are unique in that they cannot be factored further into smaller numbers, unlike composite numbers.
- For example, 15 can be expressed as 3×5, but 7 cannot be factored further.
Even and Odd Primes:
- The only even prime number is 2. All other even numbers are composite because they are divisible by 2.
- All other prime numbers are odd, as even numbers greater than 2 have more than two divisors.
Infinite Nature:
- There are infinitely many prime numbers. This was first proven by the ancient Greek mathematician Euclid.
Applications of Prime Numbers
Prime numbers are not merely abstract mathematical curiosities; they have practical significance in many fields:
Cryptography:
Modern encryption techniques, such as RSA encryption, rely heavily on the properties of large prime numbers to secure digital communication. The difficulty of factoring large numbers into primes forms the basis of cryptographic security.
Number Theory:
Primes are central to the study of integers and are used in proofs and discoveries about the properties of numbers.
Computer Algorithms:
Efficient algorithms for finding prime numbers are essential in programming, particularly in generating random numbers and optimizing computations.
Digital Security:
Prime numbers play a vital role in securing online transactions, protecting sensitive information, and ensuring data integrity.
Identifying Prime Numbers
Several methods exist to determine whether a number is prime:
- Trial Division: Divide the number by all integers up to its square root. If no divisors are found, it is prime.
- Sieve of Eratosthenes: An ancient algorithm that systematically eliminates composite numbers from a list, leaving primes.
- Primality Tests: Advanced algorithms, such as the Miller-Rabin test, are used for large numbers.
Interesting Facts About Prime Numbers
Twin Primes:
Pairs of primes that differ by 2, such as (3,5) and (11,13), are called twin primes.
Largest Known Prime:
The largest known prime numbers are often discovered using distributed computing and are typically Mersenne primes, expressed as 2n−1.
Goldbach’s Conjecture:
An unproven hypothesis states that every even integer greater than 2 is the sum of two prime numbers.
Integers, a fundamental concept in mathematics, are whole numbers that include positive numbers, negative numbers, and zero. They are denoted by the symbol Z\mathbb{Z}Z, derived from the German word Zahlen, meaning “numbers.” Integers are crucial for understanding arithmetic, algebra, and advanced mathematical concepts, serving as a foundation for both theoretical and applied mathematics.
What are Integers?
Integers are a set of numbers that include:
- Positive integers: 1,2,3,…
- Negative integers: −1,−2,−3,…
- Zero: 000
Unlike fractions or decimals, integers do not include parts or divisions of a whole number. For instance, 3 is an integer, but 3.5 is not.
Properties of Integers
Integers possess several key properties that make them indispensable in mathematics:
Closure Property:
The sum, difference, or product of two integers is always an integer. For example:
3+(−5) = −2, and 4×(−3) = −12.
Commutative Property:
- The addition and multiplication of integers are commutative, meaning the order does not affect the result:
a+b = b+a, and a×b = b×a. - However, subtraction and division are not commutative.
Associative Property:
The grouping of integers does not change the result for addition and multiplication:
(a+b)+c = a+(b+c), and (a×b)×c = a×(b×c).
Identity Element:
- The additive identity is 0, as adding zero to any integer does not change its value:
a+0 = a. - The multiplicative identity is 111, as multiplying any integer by 1 gives the same integer:
a×1 = a.
Distributive Property:
Multiplication distributes over addition or subtraction:
a×(b+c) = (a×b)+(a×c).
Representation of Integers on the Number Line
Integers can be represented on a number line, where:
- Positive integers lie to the right of zero.
- Negative integers lie to the left of zero.
- Zero serves as the central reference point.
The number line visually demonstrates the order and magnitude of integers, aiding in operations like addition and subtraction.
Applications of Integers
Integers play a vital role in various fields:
- Everyday Life: Representing temperatures, bank balances (debits and credits), and elevations (above or below sea level).
- Mathematics: Serving as the basis for operations in algebra, equations, and inequalities.
- Computer Science: Used in programming, algorithms, and data structures.
- Physics: Representing directions (positive or negative) and quantities like charges.
Importance in Advanced Mathematics
Integers are a subset of the real numbers and serve as the foundation for more complex number systems, including rational numbers, irrational numbers, and complex numbers. They are essential for exploring modular arithmetic, number theory, and cryptography.
The numeral system, the method of representing numbers, is one of humanity’s most significant inventions. It forms the foundation of mathematics and has played a pivotal role in advancing science, technology, and commerce. Over centuries, various numeral systems have evolved across cultures, reflecting diverse approaches to counting, recording, and calculating.
What is a Numeral System?
A numeral system is a set of symbols and rules used to represent numbers. At its core, it is a structured method to express quantities, perform calculations, and communicate mathematical ideas. Different numeral systems have been developed throughout history, each with its own characteristics, strengths, and limitations.
Types of Numeral Systems
Unary System:
The simplest numeral system, where a single symbol is repeated to represent numbers. For example, five would be represented as ∣∣∣∣∣. While easy to understand, this system is inefficient for representing large numbers.
Roman Numerals:
Used by ancient Romans, this system employs letters (I, V, X, L, C, D, M) to represent numbers. For example, 10 is X, and 50 is L. While widely used in historical contexts, Roman numerals are cumbersome for arithmetic operations.
Binary System:
A base-2 system using only two digits, 0 and 1. Binary is fundamental to modern computing and digital systems. For example, the binary number 101 represents 5 in the decimal system.
Decimal System:
The most commonly used numeral system today, it is a base-10 system employing digits from 0 to 9. The place value of each digit depends on its position, making it efficient for arithmetic operations and everyday use.
Other Positional Systems:
- Octal (Base-8): Uses digits 0 to 7.
- Hexadecimal (Base-16): Uses digits 0 to 9 and letters A to F to represent values 10 to 15. Common in computing and digital technology.
The Hindu-Arabic Numeral System
The Hindu-Arabic numeral system, developed in ancient India and later transmitted to Europe through Arab mathematicians, revolutionized mathematics. This base-10 system introduced the concept of zero and positional notation, which were groundbreaking innovations. The use of zero as a placeholder enabled the representation of large numbers and simplified calculations, laying the foundation for modern arithmetic and algebra.
Importance of Numeral Systems
Numeral systems are essential for:
- Mathematics and Science: Allowing precise calculations and measurements.
- Commerce: Facilitating trade, accounting, and financial transactions.
- Technology: Enabling the development of computers, algorithms, and digital systems.
- Cultural Exchange: Bridging civilizations through shared knowledge of numbers and mathematics.
Modern Applications
In the digital age, numeral systems are more relevant than ever. Binary, octal, and hexadecimal systems are integral to computer programming, data processing, and telecommunications. The decimal system remains dominant in everyday life, ensuring universal accessibility to numbers and calculations.
Quadrilaterals are one of the most fundamental shapes in geometry. Derived from the Latin words quadri (meaning four) and latus (meaning side), a quadrilateral is a polygon with four sides, four vertices, and four angles. These shapes are ubiquitous, forming the basis of many structures, patterns, and designs in both natural and human-made environments.
Definition and Properties
A quadrilateral is defined as a closed, two-dimensional shape with the following characteristics:
- Four Sides: It has exactly four edges or line segments.
- Four Vertices: The points where the sides meet.
- Four Angles: The interior angles formed by adjacent sides.
The sum of the interior angles of a quadrilateral is always 360∘360^\circ360∘. This property holds true for all quadrilaterals, irrespective of their type.
Types of Quadrilaterals
Quadrilaterals can be broadly classified into two categories: regular and irregular. Regular quadrilaterals have equal sides and angles, while irregular ones do not. Below are the most common types:
Parallelogram:
- Opposite sides are parallel and equal.
- Opposite angles are equal.
- Examples include rhombuses, rectangles, and squares.
Rectangle:
- All angles are 90°.
- Opposite sides are equal and parallel.
Square:
- A special type of rectangle where all sides are equal.
- Angles are 90°.
Rhombus:
- All sides are equal.
- Opposite angles are equal.
Trapezium (or Trapezoid):
- Only one pair of opposite sides is parallel.
Kite:
- Two pairs of adjacent sides are equal.
- Diagonals intersect at right angles.
Diagonals of Quadrilaterals
The diagonals of a quadrilateral are line segments connecting opposite vertices. They play a key role in defining the properties of the shape:
- In a parallelogram, the diagonals bisect each other.
- In a rectangle, diagonals are equal.
- In a rhombus or square, diagonals bisect each other at right angles.
Applications of Quadrilaterals
Quadrilaterals are found everywhere in our daily lives, from architectural designs to modern technology.
Architecture and Construction: Quadrilaterals form the framework of buildings, bridges, and other structures. Squares and rectangles are particularly common due to their stability and simplicity.
Art and Design: Patterns, tessellations, and artworks often rely on quadrilateral shapes for aesthetic appeal.
Technology: Quadrilateral meshes are used in computer graphics and modeling.
Transportation: Roads, signs, and pathways often incorporate quadrilateral layouts.
Geometrical Importance
Quadrilaterals are a stepping stone to understanding more complex polygons and three-dimensional shapes. Studying their properties helps in solving problems related to area, perimeter, and symmetry, making them vital in mathematics and geometry.
Perfect numbers are a fascinating concept in mathematics, admired for their unique properties and deep connections to number theory. These numbers are as mysterious as they are beautiful, inspiring curiosity and exploration among mathematicians for centuries.
What Are Perfect Numbers?
A perfect number is a positive integer that equals the sum of its proper divisors, excluding itself. Proper divisors are numbers that divide the number evenly, apart from the number itself.
For example:
- The divisors of 6 are 1,2, and 3. The sum of these divisors is 1+2+3=6, making 6 a perfect number.
- Similarly, 28 is perfect because its divisors 1,2,4,7, and 14 add up to 28.
Properties of Perfect Numbers
Even Nature:
- All known perfect numbers are even. It remains an open question in mathematics whether odd perfect numbers exist.
Connection with Mersenne Primes:
- Perfect numbers are closely linked to Mersenne primes, which are prime numbers of the form 2n−1.
- The formula for generating even perfect numbers is:
N = 2n−1×(2n−1),
where 2n−1 is a Mersenne prime. - For instance, when n = 2, 22−1 = 3 (a Mersenne prime), and the perfect number is 22−1×3 = 6.
Abundance and Deficiency:
- Numbers are classified as abundant, deficient, or perfect based on the sum of their divisors. Perfect numbers are rare and represent a balance between abundance and deficiency.
Examples of Perfect Numbers
The first few perfect numbers are:
- 6
- 28
- 496
- 8128
These numbers grow rapidly in size, with each subsequent perfect number being significantly larger than the previous one.
Historical Context
The concept of perfect numbers dates back to ancient Greek mathematics. Euclid, in his seminal work Elements, established the connection between perfect numbers and Mersenne primes. Centuries later, Swiss mathematician Leonhard Euler proved that every even perfect number can be expressed using Euclid’s formula, solidifying the link between the two.
Applications of Perfect Numbers
While perfect numbers are primarily studied for their theoretical significance, they have applications in areas such as:
Cryptography: The connection between perfect numbers and Mersenne primes is crucial in modern encryption algorithms.
Number Theory: Perfect numbers provide insights into the properties of divisors and the structure of integers.
Recreational Mathematics: They are a source of curiosity and exploration, encouraging mathematical inquiry.
Open Questions and Mysteries
Odd Perfect Numbers: Despite centuries of research, no odd perfect number has been discovered. If they exist, they must be extraordinarily large.
Infinitude of Perfect Numbers: It is unknown whether there are infinitely many perfect numbers, though many mathematicians suspect there are.
Odd numbers are a fascinating and fundamental part of mathematics. Recognized for their distinct properties and behavior, odd numbers form an integral subset of integers and play an important role in arithmetic, algebra, and number theory. Their unique nature sparks curiosity and contributes to various applications in mathematics and beyond.
What Are Odd Numbers?
Odd numbers are integers that cannot be evenly divided by 2. In other words, when an odd number is divided by 2, it leaves a remainder of 1. Examples of odd numbers include 1,3,5,7,9,11,…. Odd numbers alternate with even numbers on the number line, creating a rhythmic sequence of integers.
Mathematically, odd numbers can be expressed in the general form:
n = 2k+1,
where k is an integer.
Properties of Odd Numbers
Odd numbers possess several distinctive properties:
Addition and Subtraction:
- The sum or difference of two odd numbers is always even.
For example: 3+5 = 8. - The sum or difference of an odd number and an even number is always odd.
For example: 3+4 = 7, 9-2 = 7.
Multiplication:
- The product of two odd numbers is always odd.
For example: 3×5 = 15.
Division:
- Dividing an odd number by another odd number does not guarantee an odd quotient. For instance, 9÷3 = 3, but 15÷5 = 3 (both odd), while 15÷7 = 2.14 (not an integer).
Odd Power:
- Raising an odd number to any power results in an odd number.
For example: 33 = 27, 52 = 25.
Representation on the Number Line
Odd numbers alternate with even numbers on the number line, creating a clear pattern. The sequence of odd numbers is infinite and can be seen as 1,3,5,7,9,…extending indefinitely in both positive and negative directions.
Applications of Odd Numbers
Odd numbers have widespread applications in various fields:
- Mathematics: Used in sequences and series, as well as solving problems in number theory.
- Computer Science: Employed in algorithms, coding patterns, and data structuring.
- Art and Design: Odd numbers are often used in aesthetics, as they provide a sense of balance and harmony.
- Daily Life: Odd numbers appear when grouping items, distributing resources, and performing other practical tasks.
Interesting Facts About Odd Numbers
- Prime Odd Numbers: All prime numbers, except 2, are odd. This is because 2 is the only even prime number, as every other even number is divisible by 2.
- Odd Magic Squares: In mathematics, magic squares often rely on odd numbers to create symmetrical and intriguing patterns.
Sum of Odd Numbers: The sum of the first n odd numbers is always equal to n2.
For example: 1+3+5 = 9 = 32.
Physics concepts:
Unveiling the Secrets: Mastering Physics Through Dynamic Speed-Time Graphs
Introduction
Speed-time graphs are invaluable tools for visualizing the motion of objects over time. They offer a comprehensive view of how an object’s motion changes, helping us analyze its acceleration, deceleration, and uniform motion. In this article, we will discuss the key components of a speed-time graph in depth, understanding how they provide insight into an object’s travel through time.
The Basics: Speed vs. Time
At the core of understanding speed-time graphs is the relationship between speed and time. The x-axis of the graph represents time, while the y-axis represents speed. This arrangement allows us to track the motion of an object as it moves over time, capturing the nuances of its motion.
Interpreting the Slope
A fundamental aspect of a speed-time graph is its slope. Slope measures how fast the speed changes over time. In mathematical terms, this is the increase during the race – how much the speed changes (increase) divided by the corresponding change in time (race). Therefore, a steeper slope indicates a more rapid change in speed, which implies significant acceleration or deceleration. On the other hand, a gentle slope symbolizes a more gradual change in speed.
Uniform Motion: A Straight Line
For an object in uniform motion – when its speed remains constant – the speed-time graph takes a different form: a straight horizontal line. This line shows that the speed of the object remains the same throughout its journey. This type of speed is often seen in scenarios such as traveling at a constant velocity on a highway.
Area Under the Graph
The area covered by the speed-time graph has important meaning. It shows the distance covered by the object during the given time interval. This concept arises from the fundamental kinetic equation: distance = speed × time. When the speed is changing, the shape of the graph will create irregular areas, each of which corresponds to a different distance traveled. Calculating these areas helps us understand the total distance covered and different segments of speed during the journey.
Analyzing Acceleration and Deceleration
When a speed-time graph displays an upward sloping curve, it indicates acceleration. This means that the object is gaining momentum with time. Conversely, a downward sloping curve represents recession – slowing down. These curves provide insight into the behavior of an object, showing how its speed changes in response to external forces.
Conclusion
Speed-time graphs are invaluable tools for visualizing the complex interplay between speed and time during the motion of an object. By interpreting the slope, identifying uniform motion, and calculating the area under the graph, we gain an overall understanding of the object’s travel. These graphs provide insight into acceleration, deceleration, and patterns of motion, making them indispensable tools in the world of physics and motion analysis. So, the next time you encounter a motion-time graph, remember the wealth of information it contains about an object’s dynamic travel through time.
The Hidden Force: Unraveling the Secrets of Relative Density in Fluid Mechanics
Introduction
In the fields of physics and materials science, relative density is a fundamental concept that helps to understand the properties of various substances. Also known as specific gravity, relative density is a metric that determines the density of a substance relative to the density of another substance, often water. This article throws light upon the essence of relative density, its formula, SI unit, dimensional formula and its relation with density and specific gravity.
What is Relative Density?
Relative density is defined as the ratio of the density of a substance to the density of a reference substance, usually water. Mathematically, it can be expressed as:
Relative Density = Density of Substance / Density of Reference Substance
Relative Density Formula
The formula for relative density is straightforward. It is the quotient of the density of the material in question divided by the density of the reference substance. Mathematically, it can be represented as:
Relative Density (RD) = Density of Substance / Density of Reference Substance
SI Unit of Relative Density
The SI unit of density is the kilogram per cubic meter (kg/m²). Since relative density is a dimensionless quantity, it has no SI units. It is the ratio of two densities with the same units, resulting in the units canceling out.
The Dimensional Formula of Relative Density
The dimensional formula for relative density is simply [M^0 L^0 T^0] , where M represents mass, L represents length, and T represents time. This reinforces the concept that relative density is a unitless quantity.
Specific Gravity and Density Relation
Specific gravity is often confused with relative density, but they are closely related. Specific gravity is a special case of relative density where the reference substance is water. Thus, the specific gravity can be calculated using the formula:
Specific Gravity = Density of Substance / Density of Water
The relationship between specific gravity and density is clear in this formula. Since the density of water is constant, the specific gravity is essentially the ratio of the density of the substance to the density of water.
Conclusion
In conclusion, relative density is an important parameter in the world of materials science and physics. It provides insight into how dense a substance is compared to a reference substance, often water. The formula, SI unit, and dimensional formula of relative density explain its essential properties, and highlight that it is a dimensionless quantity. Furthermore, the relationship between specific gravity and density shows its practical applications in various fields. As scientists and researchers continue to explore the properties of various materials, the concept of relative density remains a cornerstone for understanding their physical properties.
Electromagnetism Decoded: Cracking Open the Secrets Behind Modern Miracles
Introduction
Electromagnetism, a fundamental force of nature, is a phenomenon that governs a wide range of physical processes and technological applications. This fascinating field includes everything from the creation of powerful electromagnets to the propagation of electromagnetic waves across vast expanses of the electromagnetic spectrum. In this article, we’ll cover the key concepts of electromagnetism, including electromagnetic waves, electromagnetic induction, and the fascinating world of electromagnets.
Electromagnetic Waves: Illuminating the Spectrum
At the heart of electromagnetism lies the electromagnetic spectrum, a continuum of electromagnetic waves characterized by varying wavelengths and frequencies. This spectrum extends from the long wavelength radio waves to the incredibly short wavelength gamma rays. These waves play an integral role in telecommunications, with radio waves facilitating wireless communication and microwaves enabling rapid data transmission. Meanwhile, the visible light portion of the spectrum allows us to perceive the world around us, which underlies the interplay between electromagnetic waves and human perception.
Electromagnetic Induction: Unveiling a Force of Change
The concept of electromagnetic induction, first discovered by Michael Faraday in the 19th century, has revolutionized the way electricity is generated. In this, an electromotive force (EMF) or voltage is produced in a conductor when exposed to a changing magnetic field. This principle forms the basis of the electric generator, where mechanical energy is converted into electrical energy through the motion of a conductive loop within a magnetic field. Electromagnetic induction is also used in devices such as transformers, which facilitate the transmission of electrical energy over long distances with minimal loss.
Electromagnets: Crafting Strength from Electric Currents
An electromagnet is a temporary magnet made by passing electric current through a coil of wire. This innovative concept, championed by William Sturgeon in the early 19th century, has led to transformative technological advances. Electromagnets are used in a variety of industries from manufacturing to medicine. For example, magnetic resonance imaging (MRI) machines use powerful electromagnets to generate detailed images of the human body, which aid in medical diagnosis without harmful radiation.
What is an Electromagnet: Unraveling the Mechanics
An electromagnet works on the principle that an electric current produces a magnetic field around a conductor. This magnetic field, in turn, magnetizes surrounding materials, creating a temporary magnet. The strength of the electromagnet can be adjusted by changing the current flowing in the coil of wire or by changing the number of turns in the coil. This flexibility makes electromagnets an invaluable tool in areas such as recycling, where they are used to separate ferrous materials from non-ferrous materials.
Conclusion
Electromagnetism is a testament to the complex relationship between electricity and magnetism. From the vast electromagnetic spectrum that surrounds us to the simple applications of electromagnetic induction and the versatility of electromagnets, this field has shaped the modern world in profound ways. As our understanding of electromagnetism deepens, we can only look forward to further breakthroughs that will spur innovation and open new frontiers in science and technology.
From Spin to Orbit: Decoding the Secrets of Rotation and Revolution
Introduction: Unveiling the Dance of Earth’s Rotation and Revolution
The celestial ballet performed by our planet, Earth, involves two fundamental movements that shape our daily lives and the changing seasons: rotation and revolution. These complex motions have profound effects on our planet’s climate, geography, and the passage of time. In this article, we take an in-depth look at the concepts of rotation and revolution, highlight their differences, examine their effects, and provide a clear understanding of their significance.
Understanding Rotation and Revolution: What Sets Them Apart
Rotation: Spinning on its Axis
Rotation refers to the movement of the Earth around its axis, which is an imaginary line that runs from the North Pole to the South Pole. This rotation is responsible for the change of day and night. As the Earth rotates, different parts of its surface are exposed to sunlight, creating a cycle of day and night. The Earth takes about 24 hours to complete one complete rotation, giving us the day-night cycle.
Revolution: The Orbital Dance around the Sun
Revolution, on the other hand, involves the Earth’s travel around the Sun in an elliptical orbit. This proposal takes approximately 365.25 days to complete, giving rise to the concept of a year. As the Earth rotates around the Sun, we experience changes in weather due to the varying distances and tilts of its axis.
Difference between Rotation and Revolution
The main difference between rotation and revolution lies in the axis around which each motion occurs. Rotation involves the Earth’s rotation on its axis, causing the cycle of day and night, while revolution is the Earth’s orbital motion around the Sun, marking the passing of the seasons and years.
Effects of Rotation and Revolution: Shaping Our World
Day-Night Cycle and Its Impact
The rotation of the earth creates the cycle of day and night. As it rotates, sunlight illuminates different parts of the planet’s surface, allowing photosynthesis, temperature changes, and human activities influenced by daylight.
Seasonal Changes and Climate Patterns
The Earth’s rotation around the Sun is responsible for the changing seasons. The tilt of the Earth’s axis results in sunlight arriving at different angles throughout the year, creating distinct climate patterns associated with each season. This phenomenon affects agriculture, wildlife behavior and even human mood and activities.
Conclusion: The Eternal Dance Continues
In the grand cosmic display of our universe, Earth’s rotation and rotation play a major role. Rotation brings the rhythm of day and night, while revolution paints the canvas of the changing seasons. These intertwined activities are not only scientific phenomena but also forces that shape the fabric of our existence. From the simplest daily routines to complex ecosystems, the effects of rotation and revolution remind us that we are part of an amazing dance that has been going on for billions of years.
Unveiling the Earth’s Hidden Secrets: Journey through its Multi-layered Marvels
Introduction
Earth, our home, is a fascinating and complex planet made up of different layers, each of which has different properties and characteristics. These layers play an important role in shaping the geological processes of the planet, from earthquakes to volcanic eruptions. In this article, we will delve deeper into the layers of the Earth, reveal their secrets and understand their importance.
How Many Layers of the Earth Are There?
The Earth is made up of four main layers: the crust, the mantle, the outer core, and the inner core. These layers are differentiated on the basis of their physical and chemical properties, temperature and state of matter. To better visualize these layers, see Layers of the Earth diagram.
The Crust: The Earth’s Thin Skin
The outermost layer of the Earth is known as the Earth’s crust. It is the thinnest layer of the Earth, accounting for only a small part of the total volume of the planet. The crust is divided into two types: continental crust and oceanic crust. Continental crust is thicker and less dense than oceanic crust, which is mainly composed of granitic rocks. On the other hand, oceanic crust mainly consists of basalt rocks and is relatively thin.
The Mantle: A Viscous Layer of Convective Flow
Beneath the crust lies the mantle, a layer that extends to a depth of about 2,900 km. The mantle is responsible for the movement of tectonic plates and is characterized by its semi-solid, plastic-like behavior. This layer experiences convection currents, which contribute to the movement of Earth’s lithospheric plates and drive geological events such as earthquakes and volcanic activity.
The Outer Core: Where Liquid Iron Flows
Beneath the mantle is the outer core, which extends from about 2,900 to 5,150 kilometers below the Earth’s surface. The outer core is a liquid layer composed mainly of iron and nickel. It plays an important role in generating the Earth’s magnetic field through the process of convection and movement of molten metals.
The Inner Core: A Sphere of Solid Iron
At the very center of the Earth lies the inner core, which extends from a depth of 5,150 kilometers to the Earth’s center, at a depth of approximately 6,371 kilometers. Despite extreme pressure, the inner core remains solid due to the high temperatures and the presence of iron and nickel in the crystalline state.
Conclusion
Understanding the Earth’s layers is essential to understanding the dynamic geological processes that shape our planet. From the thinnest outer layer to the innermost core, each layer contributes to Earth’s unique characteristics. Earth’s water-holding layer, found primarily in the mantle, influences various phenomena such as volcanic eruptions and the movement of tectonic plates. As we continue to explore and study the layers of our planet, we gain insight into the complex interplay of forces that have shaped the Earth over millions of years.
Unveiling the Intrigue of Magnetic Dipole Moments: Unlocking the Secrets of Attraction and Repulsion
Introduction
The magnetic dipole moment is a fundamental concept in physics that plays an important role in understanding the behavior of magnetic materials and electromagnetic phenomena. It describes the strength and orientation of a magnetic dipole, which is a small magnetic object that has north and south poles, similar to a bar magnet. In this article, we will learn in detail about the magnetic dipole moment, its formula, SI unit and its importance in various contexts.
What is Magnetic Dipole Moment?
Magnetic dipole moment refers to the product of the strength of a magnetic dipole and the distance between its poles. Mathematically, it can be expressed as:
μ = m × r
Where:
– μ is the magnetic dipole moment,
– m is the strength of the magnetic dipole (pole strength), and
– r is the distance between the poles of the dipole.
Formula of Magnetic Dipole Moment
As shown above, the magnetic dipole moment formula is simple and straightforward. This highlights the direct proportionality between the strength of a dipole and the distance between its poles. This formula is a fundamental equation used to calculate the magnetic dipole moment of various magnetic objects.
SI Unit of Magnetic Dipole Moment
The SI unit of magnetic dipole moment is the ampere-metre squared (A m²). This unit is derived from the SI base units of current (A) and length (m). When the pole strength is in amperes and the distance is in meters, the resulting magnetic dipole moment will be in amperes per meter squared.
Magnetic Dipole Moment of a Revolving Electron
An electron moving around the nucleus exhibits angular momentum, which gives rise to its magnetic dipole moment. The formula for the magnetic dipole moment of a rotating electron is given as:
μ = (e × A) / (2 × m)
Where:
– μ is the magnetic dipole moment,
– e is the charge of the electron,
– A is the area of the circular path the electron follows, and
– m is the mass of the electron.
Significance of Magnetic Dipole Moment
The concept of magnetic dipole moment holds immense importance in various fields of physics and engineering. It forms the basis for understanding the behavior of magnetic materials, electromagnetic induction, and even the Earth’s magnetic field. The magnetic dipole moments of particles, such as electrons, contribute to the creation of magnetic forces and are essential in the design of technologies such as magnetic resonance imaging (MRI) machines.
Conclusion
In conclusion, the magnetic dipole moment is an important concept that underlies many magnetic phenomena and technologies. Its formula, SI units and applications in various fields reflect its fundamental importance in the world of physics. Be it the magnetic dipole moment of a spinning electron or the behavior of magnetic materials, this concept enables us to understand and harness the power of magnetism in our modern world.