Set theory, introduced by the German mathematician Georg Cantor in the late 19th century, is a branch of mathematics that deals with the study of sets. A set is a well-defined collection of distinct objects, which can be numbers, symbols, or even other sets. This fundamental theory underpins many areas of mathematics and logic, providing a framework for understanding and organizing mathematical concepts.
What is a Set?
A set is typically represented using curly brackets, with its elements listed inside. For example:
- A = {1,2,3} is a set of numbers.
- B = {apple, banana, cherry} is a set of fruits.
The elements of a set are distinct and unordered. Sets can be finite, like {1,2,3}, or infinite, like the set of all natural numbers N = {1,2,3,… }
Basic Notations and Terms
Subset:
A set A is a subset of set B if every element of A is also an element of B. This is denoted as A⊆B.
Union:
The union of two sets A and B contains all elements that are in A, B, or both.
A∪B = {x∣x∈A or x∈B}.
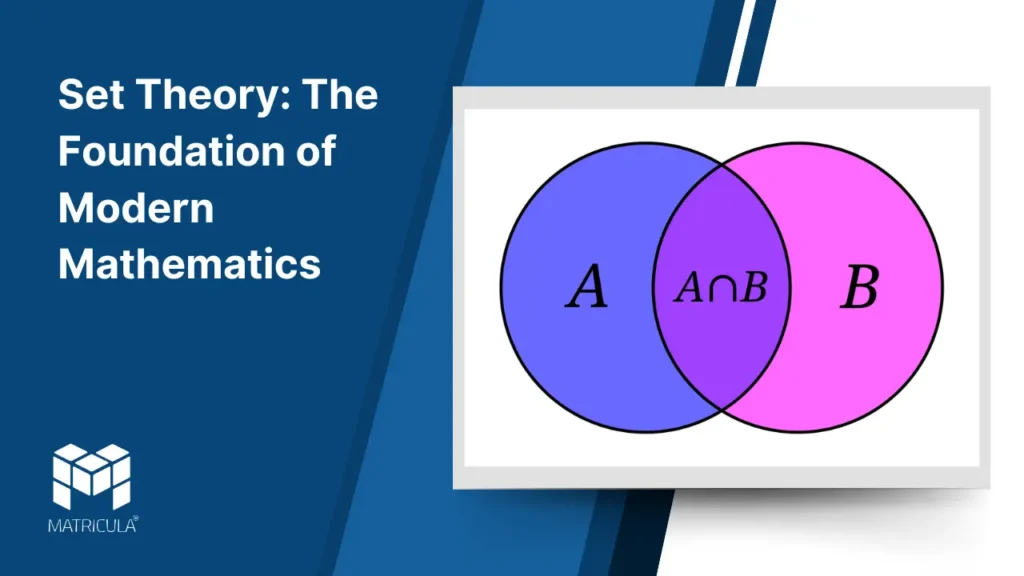
Intersection:
The intersection of A and B includes elements that are common to both sets.
A∩B = {x∣x∈A and x∈B}.
Difference:
The difference of A and B contains elements in A that are not in B.
A−B = {x∣x∈A and x∉B}.
Complement:
The complement of A includes all elements not in A, relative to a universal set U.
Ac=U−A.
Empty Set:
The empty set, denoted by ∅ or {}, contains no elements.
Importance of Set Theory
Set theory forms the basis of many mathematical disciplines, including algebra, geometry, calculus, and topology. It provides a language to describe and analyze mathematical structures systematically.
Applications of Set Theory
Mathematics:
Set theory is used in defining functions, relations, and spaces. Concepts like intersections and unions are vital in probability and statistics.
Logic and Computer Science:
- In logic, sets are essential for understanding propositions and truth tables.
- In computer science, set theory is used in database operations, programming languages, and algorithms.
Data Analysis:
Sets help organize and analyze data, making it easier to find commonalities or differences between datasets.
Artificial Intelligence:
AI systems often rely on set-based operations for classification and decision-making.
Historical Context
Georg Cantor’s pioneering work on sets was initially controversial but eventually revolutionized mathematics. His ideas on infinite sets and cardinality introduced concepts like countable and uncountable infinities, which expanded the horizons of mathematical thought.
Challenges and Paradoxes
Set theory is not without its complexities. Certain paradoxes, such as Russell’s Paradox, challenge the traditional understanding of sets. These issues have led to the development of axiomatic set theory, such as Zermelo-Fraenkel set theory, which provides a rigorous foundation for the discipline.