Triangles are among the simplest yet most fascinating shapes in geometry, offering numerous properties and applications. One of the core concepts associated with triangles is congruence. When two triangles are congruent, they are identical in shape and size, though their orientation or position might differ. Understanding the congruence of triangles forms the foundation for solving many geometrical problems and is a crucial aspect of mathematical reasoning.
What is Congruence of Triangles?
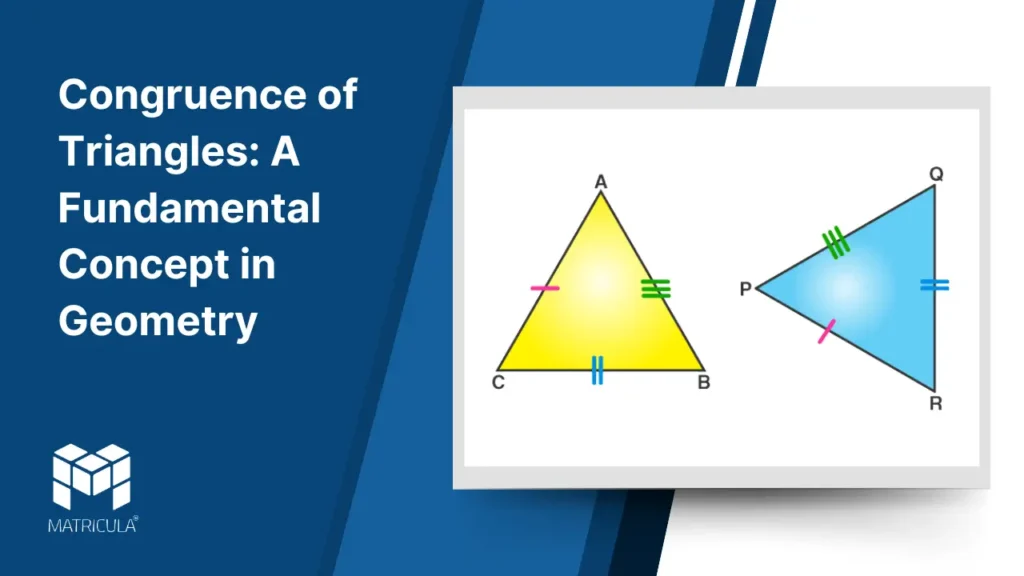
Two triangles are said to be congruent if all their corresponding sides and angles are equal. This means that if one triangle is superimposed on the other, they will perfectly overlap, matching each other exactly. Congruent triangles are denoted using the symbol ≅. For example, if △ABC≅△PQR, it implies:
- AB = PQ, BC = QR, AC = PR (corresponding sides are equal).
- ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R (corresponding angles are equal).
Criteria for Triangle Congruence
To determine whether two triangles are congruent, it is not necessary to compare all six elements (three sides and three angles). Several criteria simplify this process:
SSS (Side-Side-Side) Criterion:
Two triangles are congruent if all three sides of one triangle are equal to the corresponding sides of the other triangle.
SAS (Side-Angle-Side) Criterion:
Two triangles are congruent if two sides and the included angle of one triangle are equal to the corresponding sides and included angle of the other triangle.
ASA (Angle-Side-Angle) Criterion:
Two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding angles and included side of the other triangle.
AAS (Angle-Angle-Side) Criterion:
Two triangles are congruent if two angles and a non-included side of one triangle are equal to the corresponding angles and side of the other triangle.
RHS (Right-Angle-Hypotenuse-Side) Criterion:
Two right-angled triangles are congruent if the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle.
Applications of Triangle Congruence
Congruence of triangles has widespread applications in geometry and beyond:
- Proving Properties: Many theorems in geometry, such as the base angles of an isosceles triangle being equal, rely on the concept of congruence.
- Construction: Architects and engineers use congruence to design structures with precise measurements and symmetry.
- Real-World Measurements: In navigation, land surveying, and map-making, congruent triangles help establish distances and angles accurately.
Practical Example
Consider a situation where you need to prove that two bridges with triangular supports are identical in design. By verifying that the corresponding sides and angles of the triangular frames are equal, you can demonstrate their congruence using one of the criteria.