The chapter “Right Circular Cylinder” introduces students to one of the most commonly used 3D geometric solids found in real life — from water pipes and cans to storage tanks. In this chapter, students will learn about the structure, surface areas, curved surface area, total surface area, and volume of a right circular cylinder.
What is a Right Circular Cylinder?
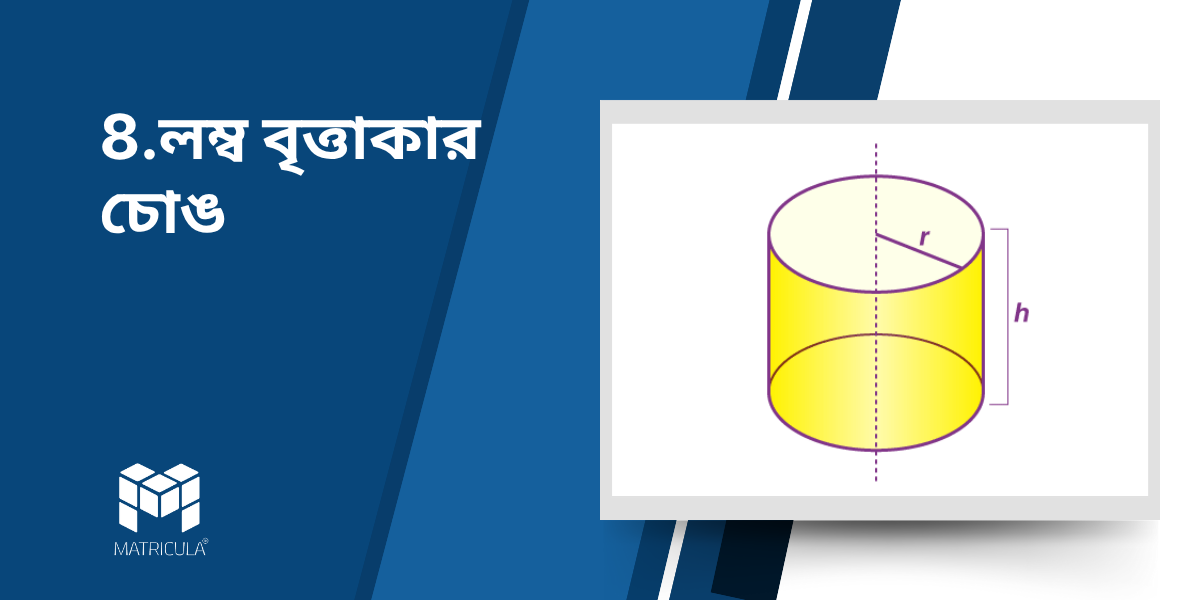
A Right Circular Cylinder (লম্ব বৃত্তাকার চোঙ) is a 3D geometric solid formed by revolving a rectangle about one of its sides (which becomes the axis). It has two parallel circular bases and a curved lateral surface.
Key Characteristics:
- Two parallel circular bases of equal radius.
- The axis is the line segment joining the centers of the two circular bases.
- The height (h) is the perpendicular distance between the bases.
- Radius (r) is the radius of the circular base.
- The curved surface joins the boundaries of the two circular faces.
Important Formulae in the Chapter
Students must understand and memorize the following standard formulae as they are foundational for solving problems in the exercises:
1. Curved Surface Area (CSA)
CSA=2πrh
The curved surface area refers to the area of the side surface that wraps around the cylinder.
2. Total Surface Area (TSA)
TSA=2πr(h+r)
This includes the CSA plus the area of the two circular bases.
3. Volume of a Right Circular Cylinder
V=πr2h
The volume is the space enclosed within the cylinder. It’s measured in cubic units and is crucial in real-life applications like determining the capacity of a tank.
Conceptual Understanding with Examples
Example 1: Curved Surface Area
Question: Find the curved surface area of a cylinder with radius 5 cm and height 10 cm.
Solution:
CSA=2πrh=2×227×5×10=72200≈314.29 cm2
The curved surface area is approximately 314.29 cm².
Example 2: Total Surface Area
Question: A closed cylindrical container has radius 7 cm and height 14 cm. Find the total surface area.
Solution:
TSA=2πr(h+r)=2×227×7×(14+7)=2×722×7×21=924 cm2
So, the total surface area is 924 cm².
Example 3: Volume
Question: Find the volume of a cylinder with radius 3 cm and height 7 cm.
Solution:
V=πr2h=227×32×7=722×9×7=198 cm3
Hence, the volume is 198 cm³.
Real-Life Applications
- Water Tanks: Used to store water in cylindrical tanks — calculation of volume helps in determining capacity.
- Cylindrical Containers: Used in packaging (e.g., cold drink cans, jars), requiring surface area to determine labeling size.
- Construction Materials: Pipes, concrete pillars, and storage drums all use cylindrical forms.
- Industrial Design: Engineers use volume and surface area to estimate material use and cost efficiency.
Common Questions and Mistakes
Misunderstanding Between CSA and TSA
Many students confuse CSA with TSA. Remember:
- CSA = only the side area (no base included)
- TSA = CSA + area of both circular bases
Units Confusion
Always use the same units for radius and height. If radius is in cm, height must also be in cm before applying formulae.
Exercises and Problem Solving
The textbook provides both numerical and application-based questions. Some require direct formula application, while others may involve reverse calculation (e.g., finding height when volume is given).
Key types of problems include:
- Finding CSA, TSA, Volume from given radius and height
- Determining one unknown dimension (radius or height) given the other and volume/surface area
- Real-world word problems involving cost calculation based on surface area (e.g., cost of painting a cylinder)
Tips to Solve Problems Efficiently
- Draw the figure: Visualizing the cylinder helps in identifying radius and height.
- Label clearly: Write all known values before applying formulae.
- Memorize π values: Use π = 227 unless asked to keep π in the final answer.
- Cross-check units: Ensure consistency in units before solving.
Conclusion
The chapter on Right Circular Cylinder is a practical and essential component of Class 10 Geometry. It builds spatial understanding and introduces students to real-life mathematical applications. By mastering the formulae, understanding the structure, and